Fluid Dynamics

• 1.I.6G

  Fluid Dynamics

  Part IB, 2001

  Determine the pressure at a depth $z$ below the surface of a static fluid of density $\rho$ subject to gravity $g$. A rigid body having volume $V$ is fully submerged in such a fluid. Calculate the buoyancy force on the body.

  An iceberg of uniform density $\rho_{I}$ is observed to float with volume $V_{I}$ protruding above a large static expanse of seawater of density $\rho_{w}$. What is the total volume of the iceberg?

  comment

• 1.II.15G

  Fluid Dynamics

  Part IB, 2001

  A fluid motion has velocity potential $\phi(x, y, t)$ given by

  $$\phi=\epsilon y \cos (x-t)$$

  where $\epsilon$ is a constant. Find the corresponding velocity field $\mathbf{u}(x, y, t)$. Determine $\nabla \cdot \mathbf{u}$.

  The time-average of a quantity $\psi(x, y, t)$ is defined as $\frac{1}{2 \pi} \int_{0}^{2 \pi} \psi(x, y, t) d t$.

  Show that the time-average of this velocity field at every point $(x, y)$ is zero.

  Write down an expression for the fluid acceleration and find the time-average acceleration at $(x, y)$.

  Suppose now that $|\epsilon| \ll 1$. The material particle at $(0,0)$ at time $t=0$ is marked with dye. Write down equations for its subsequent motion and verify that its position $(x, y)$ at time $t>0$ is given (correct to terms of order $\epsilon^{2}$ ) as

  $$\begin{aligned} &x=\epsilon^{2}\left(\frac{1}{2} t-\frac{1}{4} \sin 2 t\right) \\ &y=\epsilon \sin t \end{aligned}$$

  Deduce the time-average velocity of the dyed particle correct to this order.

  comment

• 3.I.8G

  Fluid Dynamics

  Part IB, 2001

  Inviscid incompressible fluid occupies the region $y>0$, which is bounded by a rigid barrier along $y=0$. At time $t=0$, a line vortex of strength $\kappa$ is placed at position $(a, b)$. By considering the flow due to an image vortex at $(a,-b)$, or otherwise, determine the velocity potential in the fluid.

  Derive the position of the original vortex at time $t>0$.

  comment

• 3.II.18G

  Fluid Dynamics

  Part IB, 2001

  State the form of Bernoulli's theorem appropriate for an unsteady irrotational motion of an inviscid incompressible fluid.

  A circular cylinder of radius $a$ is immersed in unbounded inviscid fluid of uniform density $\rho$. The cylinder moves in a prescribed direction perpendicular to its axis, with speed $U$. Use cylindrical polar coordinates, with the direction $\theta=0$ parallel to the direction of the motion, to find the velocity potential in the fluid.

  If $U$ depends on time $t$ and gravity is negligible, determine the pressure field in the fluid at time $t$. Deduce the fluid force per unit length on the cylinder.

  [In cylindrical polar coordinates, $\nabla \phi=\frac{\partial \phi}{\partial r} \mathbf{e}_{r}+\frac{1}{r} \frac{\partial \phi}{\partial \theta} \mathbf{e}_{\theta}$.]

  comment

• 4.I.7G

  Fluid Dynamics

  Part IB, 2001

  Starting from the Euler equation, derive the vorticity equation for the motion of an inviscid incompressible fluid under a conservative body force, and give a physical interpretation of each term in the equation. Deduce that in a flow field of the form $\mathbf{u}=(u(x, y, t), v(x, y, t), 0)$ the vorticity of a material particle is conserved.

  Find the vorticity for such a flow in terms of the stream function $\psi$. Deduce that if the flow is steady, there must be a function $f$ such that

  $$\nabla^{2} \psi=f(\psi)$$

  comment

• 4.II.16G

  Fluid Dynamics

  Part IB, 2001

  A long straight canal has rectangular cross-section with a horizontal bottom and width $w(x)$ that varies slowly with distance $x$ downstream. Far upstream, $w$ has a constant value $W$, the water depth has a constant value $H$, and the velocity has a constant value $U$. Assuming that the water velocity is steady and uniform across the channel, use mass conservation and Bernoulli's theorem, which should be stated carefully, to show that the water depth $h(x)$ satisfies

  $$\left(\frac{W}{w}\right)^{2}=\left(1+\frac{2}{F}\right)\left(\frac{h}{H}\right)^{2}-\frac{2}{F}\left(\frac{h}{H}\right)^{3} \text { where } F=\frac{U^{2}}{g H}$$

  Deduce that for a given value of $F$, a flow of this kind can exist only if $w(x)$ is everywhere greater than or equal to a critical value $w_{c}$, which is to be determined in terms of $F$.

  Suppose that $w(x)>w_{c}$ everywhere. At locations where the channel width exceeds $W$, determine graphically, or otherwise, under what circumstances the water depth exceeds $H .$

  comment

• 1.I.6C

  Fluid Dynamics

  Part IB, 2002

  A fluid flow has velocity given in Cartesian co-ordinates as $\mathbf{u}=(k t y, 0,0)$ where $k$ is a constant and $t$ is time. Show that the flow is incompressible. Find a stream function and determine an equation for the streamlines at time $t$.

  At $t=0$ the points along the straight line segment $x=0,0 \leqslant y \leqslant a, z=0$ are marked with dye. Show that at any later time the marked points continue to form a segment of a straight line. Determine the length of this line segment at time $t$ and the angle that it makes with the $x$-axis.

  comment

• 1.II.15C

  Fluid Dynamics

  Part IB, 2002

  State the unsteady form of Bernoulli's theorem.

  A spherical bubble having radius $R_{0}$ at time $t=0$ is located with its centre at the origin in unbounded fluid. The fluid is inviscid, has constant density $\rho$ and is everywhere at rest at $t=0$. The pressure at large distances from the bubble has the constant value $p_{\infty}$, and the pressure inside the bubble has the constant value $p_{\infty}-\triangle p$. In consequence the bubble starts to collapse so that its radius at time $t$ is $R(t)$. Find the velocity everywhere in the fluid in terms of $R(t)$ at time $t$ and, assuming that surface tension is negligible, show that $R$ satisfies the equation

  $$R \ddot{R}+\frac{3}{2} \dot{R}^{2}=-\frac{\triangle p}{\rho}$$

  Find the total kinetic energy of the fluid in terms of $R(t)$ at time $t$. Hence or otherwise obtain a first integral of the above equation.

  comment

• 3.I.8C

  Fluid Dynamics

  Part IB, 2002

  State and prove Kelvin's circulation theorem.

  Consider a planar flow in the unbounded region outside a cylinder for which the vorticity vanishes everywhere at time $t=0$. What may be deduced about the circulation around closed loops in the fluid at time $t$ :

  (i) that do not enclose the cylinder;

  (ii) that enclose the cylinder?

  Give a brief justification for your answer in each case.

  comment

• 3.II.18C

  Fluid Dynamics

  Part IB, 2002

  Use Euler's equation to derive Bernoulli's theorem for the steady flow of an inviscid fluid of uniform density $\rho$ in the absence of body forces.

  Such a fluid flows steadily through a long cylindrical elastic tube having circular cross-section. The variable $z$ measures distance downstream along the axis of the tube. The tube wall has thickness $h(z)$, so that if the external radius of the tube is $r(z)$, its internal radius is $r(z)-h(z)$, where $h(z) \geqslant 0$ is a given slowly-varying function that tends to zero as $z \rightarrow \pm \infty$. The elastic tube wall exerts a pressure $p(z)$ on the fluid given as

  $$p(z)=p_{0}+k[r(z)-R]$$

  where $p_{0}, k$ and $R$ are positive constants. Far upstream, $r$ has the constant value $R$, the fluid pressure has the constant value $p_{0}$, and the fluid velocity $u$ has the constant value $V$. Assume that gravity is negligible and that $h(z)$ varies sufficiently slowly that the velocity may be taken as uniform across the tube at each value of $z$. Use mass conservation and Bernoulli's theorem to show that $u(z)$ satisfies

  $$\frac{h}{R}=1-\left(\frac{V}{u}\right)^{1 / 2}+\frac{1}{4} \lambda\left[1-\left(\frac{u}{V}\right)^{2}\right], \quad \text { where } \quad \lambda=\frac{2 \rho V^{2}}{k R}$$

  Sketch a graph of $h / R$ against $u / V$. Show that if $h(z)$ exceeds a critical value $h_{c}(\lambda)$, no such flow is possible and find $h_{c}(\lambda)$.

  Show that if $h<h_{c}(\lambda)$ everywhere, then for given $h$ the equation has two positive solutions for $u$. Explain how the given value of $\lambda$ determines which solution should be chosen.

  comment

• 4.I $. 7 \mathrm{C} \quad$

  Fluid Dynamics

  Part IB, 2002

  If $\mathbf{u}$ is given in Cartesian co-ordinates as $\mathbf{u}=(-\Omega y, \Omega x, 0)$, with $\Omega$ a constant, verify that

  $$\mathbf{u} \cdot \nabla \mathbf{u}=\nabla\left(-\frac{1}{2} \mathbf{u}^{2}\right)$$

  When incompressible fluid is placed in a stationary cylindrical container of radius $a$ with its axis vertical, the depth of the fluid is $h$. Assuming that the free surface does not reach the bottom of the container, use cylindrical polar co-ordinates to find the equation of the free surface when the fluid and the container rotate steadily about this axis with angular velocity $\Omega$.

  Deduce the angular velocity at which the free surface first touches the bottom of the container.

  comment

• 4.II.16C

  Fluid Dynamics

  Part IB, 2002

  Use Euler's equation to show that in a planar flow of an inviscid fluid the vorticity $\boldsymbol{\omega}$ satisfies

  $$\frac{D \omega}{D t}=0$$

  Write down the velocity field associated with a point vortex of strength $\kappa$ in unbounded fluid.

  Consider now the flow generated in unbounded fluid by two point vortices of strengths $\kappa_{1}$ and $\kappa_{2}$ at $\mathbf{x}_{1}(t)=\left(x_{1}, y_{1}\right)$ and $\mathbf{x}_{2}(t)=\left(x_{2}, y_{2}\right)$, respectively. Show that in the subsequent motion the quantity

  $$\mathbf{q}=\kappa_{1} \mathbf{x}_{1}+\kappa_{2} \mathbf{x}_{2}$$

  remains constant. Show also that the separation of the vortices, $\left|\mathbf{x}_{2}-\mathbf{x}_{1}\right|$, remains constant.

  Suppose finally that $\kappa_{1}=\kappa_{2}$ and that the vortices are placed at time $t=0$ at positions $(a, 0)$ and $(-a, 0)$. What are the positions of the vortices at time $t$ ?

  comment

• 1.I.6C

  Fluid Dynamics

  Part IB, 2003

  An unsteady fluid flow has velocity field given in Cartesian coordinates $(x, y, z)$ by $\mathbf{u}=(1, x t, 0)$, where $t$ denotes time. Dye is released into the fluid from the origin continuously. Find the position at time $t$ of the dye particle that was released at time $s$ and hence show that the dye streak lies along the curve

  $$y=\frac{1}{2} t x^{2}-\frac{1}{6} x^{3}$$

  comment

• 1.II.15C

  Fluid Dynamics

  Part IB, 2003

  Starting from the Euler equations for incompressible, inviscid flow

  $$\rho \frac{D \mathbf{u}}{D t}=-\nabla p, \quad \nabla \cdot \mathbf{u}=0$$

  derive the vorticity equation governing the evolution of the vorticity $\boldsymbol{\omega}=\nabla \times \mathbf{u}$.

  Consider the flow

  $$\mathbf{u}=\beta(-x,-y, 2 z)+\Omega(t)(-y, x, 0)$$

  in Cartesian coordinates $(x, y, z)$, where $t$ is time and $\beta$ is a constant. Compute the vorticity and show that it evolves in time according to

  $$\boldsymbol{\omega}=\omega_{0} \mathrm{e}^{2 \beta t} \mathbf{k}$$

  where $\omega_{0}$ is the initial magnitude of the vorticity and $\mathbf{k}$ is a unit vector in the $z$-direction.

  Show that the material curve $C(t)$ that takes the form

  $$x^{2}+y^{2}=1 \quad \text { and } \quad z=1$$

  at $t=0$ is given later by

  $$x^{2}+y^{2}=a^{2}(t) \quad \text { and } \quad z=\frac{1}{a^{2}(t)},$$

  where the function $a(t)$ is to be determined.

  Calculate the circulation of $\mathbf{u}$ around $C$ and state how this illustrates Kelvin's circulation theorem.

  comment

• 3.I.8C

  Fluid Dynamics

  Part IB, 2003

  Show that the velocity field

  $$\mathbf{u}=\mathbf{U}+\frac{\boldsymbol{\Gamma} \times \mathbf{r}}{2 \pi r^{2}},$$

  where $\mathbf{U}=(U, 0,0), \mathbf{\Gamma}=(0,0, \Gamma)$ and $\mathbf{r}=(x, y, 0)$ in Cartesian coordinates $(x, y, z)$, represents the combination of a uniform flow and the flow due to a line vortex. Define and evaluate the circulation of the vortex.

  Show that

  $$\oint_{C_{R}}(\mathbf{u} \cdot \mathbf{n}) \mathbf{u} d l \rightarrow \frac{1}{2} \boldsymbol{\Gamma} \times \mathbf{U} \quad \text { as } \quad R \rightarrow \infty$$

  where $C_{R}$ is a circle $x^{2}+y^{2}=R^{2}, z=$ const. Explain how this result is related to the lift force on a two-dimensional aerofoil or other obstacle.

  comment

• 3.II.18C

  Fluid Dynamics

  Part IB, 2003

  State the form of Bernoulli's theorem appropriate for an unsteady irrotational motion of an inviscid incompressible fluid in the absence of gravity.

  Water of density $\rho$ is driven through a tube of length $L$ and internal radius $a$ by the pressure exerted by a spherical, water-filled balloon of radius $R(t)$ attached to one end of the tube. The balloon maintains the pressure of the water entering the tube at $2 \gamma / R$ in excess of atmospheric pressure, where $\gamma$ is a constant. It may be assumed that the water exits the tube at atmospheric pressure. Show that

  $$R^{3} \ddot{R}+2 R^{2} \dot{R}^{2}=-\frac{\gamma a^{2}}{2 \rho L} .$$

  Solve equation ( $\dagger$ ), by multiplying through by $2 R \dot{R}$ or otherwise, to obtain

  $$t=R_{0}^{2}\left(\frac{2 \rho L}{\gamma a^{2}}\right)^{1 / 2}\left[\frac{\pi}{4}-\frac{\theta}{2}+\frac{1}{4} \sin 2 \theta\right]$$

  where $\theta=\sin ^{-1}\left(R / R_{0}\right)$ and $R_{0}$ is the initial radius of the balloon. Hence find the time when $R=0$.

  comment

• 4.I.7C

  Fluid Dynamics

  Part IB, 2003

  Inviscid fluid issues vertically downwards at speed $u_{0}$ from a circular tube of radius a. The fluid falls onto a horizontal plate a distance $H$ below the end of the tube, where it spreads out axisymmetrically.

  Show that while the fluid is falling freely it has speed

  $$u=u_{0}\left[1+\frac{2 g}{u_{0}^{2}}(H-z)\right]^{1 / 2}$$

  and occupies a circular jet of radius

  $$R=a\left[1+\frac{2 g}{u_{0}^{2}}(H-z)\right]^{-1 / 4},$$

  where $z$ is the height above the plate and $g$ is the acceleration due to gravity.

  Show further that along the plate, at radial distances $r \gg a$ (i.e. far from the falling jet), where the fluid is flowing almost horizontally, it does so as a film of height $h(r)$, where

  $$\frac{a^{4}}{4 r^{2} h^{2}}=1+\frac{2 g}{u_{0}^{2}}(H-h)$$

  comment

• 4.II.16C

  Fluid Dynamics

  Part IB, 2003

  Define the terms irrotational flow and incompressible flow. The two-dimensional flow of an incompressible fluid is given in terms of a streamfunction $\psi(x, y)$ as

  $$\mathbf{u}=(u, v)=\left(\frac{\partial \psi}{\partial y},-\frac{\partial \psi}{\partial x}\right)$$

  in Cartesian coordinates $(x, y)$. Show that the line integral

  $$\int_{\mathbf{x}_{1}}^{\mathbf{x}_{\mathbf{2}}} \mathbf{u} \cdot \mathbf{n} d l=\psi\left(\mathbf{x}_{\mathbf{2}}\right)-\psi\left(\mathbf{x}_{\mathbf{1}}\right)$$

  along any path joining the points $\mathbf{x}_{\mathbf{1}}$ and $\mathbf{x}_{\mathbf{2}}$, where $\mathbf{n}$ is the unit normal to the path. Describe how this result is related to the concept of mass conservation.

  Inviscid, incompressible fluid is contained in the semi-infinite channel $x>0$, $0<y<1$, which has rigid walls at $x=0$ and at $y=0,1$, apart from a small opening at the origin through which the fluid is withdrawn with volume flux $m$ per unit distance in the third dimension. Show that the streamfunction for irrotational flow in the channel can be chosen (up to an additive constant) to satisfy the equation

  $$\frac{\partial^{2} \psi}{\partial x^{2}}+\frac{\partial^{2} \psi}{\partial y^{2}}=0$$

  and boundary conditions

  if it is assumed that the flow at infinity is uniform. Solve the boundary-value problem above using separation of variables to obtain

  $$\psi=-m y+\frac{2 m}{\pi} \sum_{n=1}^{\infty} \frac{1}{n} \sin n \pi y e^{-n \pi x}$$

  $$\begin{aligned} & \psi=0 \quad \text { on } y=0, x>0, \\ & \psi=-m \quad \text { on } x=0,0<y<1, \\ & \psi=-m \quad \text { on } y=1, x>0, \\ & \psi \rightarrow-m y \quad \text { as } x \rightarrow \infty, \end{aligned}$$

  comment

• 1.I.9C

  Fluid Dynamics

  Part IB, 2004

  From the general mass-conservation equation, show that the velocity field $\mathbf{u}(\mathbf{x})$ of an incompressible fluid is solenoidal, i.e. that $\nabla \cdot \mathbf{u}=0$.

  Verify that the two-dimensional flow

  $$\mathbf{u}=\left(\frac{y}{x^{2}+y^{2}}, \frac{-x}{x^{2}+y^{2}}\right)$$

  is solenoidal and find a streamfunction $\psi(x, y)$ such that $\mathbf{u}=(\partial \psi / \partial y,-\partial \psi / \partial x)$.

  comment

• 1.II.20C

  Fluid Dynamics

  Part IB, 2004

  A layer of water of depth $h$ flows along a wide channel with uniform velocity $(U, 0)$, in Cartesian coordinates $(x, y)$, with $x$ measured downstream. The bottom of the channel is at $y=-h$, and the free surface of the water is at $y=0$. Waves are generated on the free surface so that it has the new position $y=\eta(x, t)=a e^{i(\omega t-k x)}$.

  Write down the equation and the full nonlinear boundary conditions for the velocity potential $\phi$ (for the perturbation velocity) and the motion of the free surface.

  By linearizing these equations about the state of uniform flow, show that

  where $g$ is the acceleration due to gravity.

  Hence, determine the dispersion relation for small-amplitude surface waves

  $$(\omega-k U)^{2}=g k \tanh k h .$$

  comment

• 3.I.10C

  Fluid Dynamics

  Part IB, 2004

  State Bernoulli's equation for unsteady motion of an irrotational, incompressible, inviscid fluid subject to a conservative body force $-\nabla \chi$.

  A long vertical U-tube of uniform cross section contains an inviscid, incompressible fluid whose surface, in equilibrium, is at height $h$ above the base. Derive the equation

  $$h \frac{d^{2} \zeta}{d t^{2}}+g \zeta=0$$

  governing the displacement $\zeta$ of the surface on one side of the U-tube, where $t$ is time and $g$ is the acceleration due to gravity.

  $$\begin{aligned} & \frac{\partial \eta}{\partial t}+U \frac{\partial \eta}{\partial x}=\frac{\partial \phi}{\partial y}, \quad \frac{\partial \phi}{\partial t}+U \frac{\partial \phi}{\partial x}+g \eta=0 \quad \text { on } \quad y=0 \\ & \frac{\partial \phi}{\partial y}=0 \quad \text { on } \quad y=-h, \end{aligned}$$

  comment

• 3.II.21C

  Fluid Dynamics

  Part IB, 2004

  Use separation of variables to determine the irrotational, incompressible flow

  $$\mathbf{u}=U \frac{a^{3}}{r^{3}}\left(\cos \theta \mathbf{e}_{r}+\frac{1}{2} \sin \theta \mathbf{e}_{\theta}\right)$$

  around a solid sphere of radius $a$ translating at velocity $U$ along the direction $\theta=0$ in spherical polar coordinates $r$ and $\theta$.

  Show that the total kinetic energy of the fluid is

  $$K=\frac{1}{4} M_{f} U^{2},$$

  where $M_{f}$ is the mass of fluid displaced by the sphere.

  A heavy sphere of mass $M$ is released from rest in an inviscid fluid. Determine its speed after it has fallen through a distance $h$ in terms of $M, M_{f}, g$ and $h$.

  comment

• 4.I.8C

  Fluid Dynamics

  Part IB, 2004

  Write down the vorticity equation for the unsteady flow of an incompressible, inviscid fluid with no body forces acting.

  Show that the flow field

  $$\mathbf{u}=(-x, x \omega(t), z-1)$$

  has uniform vorticity of magnitude $\omega(t)=\omega_{0} e^{t}$ for some constant $\omega_{0}$.

  comment

• 4.II.18C

  Fluid Dynamics

  Part IB, 2004

  Use Euler's equation to derive the momentum integral

  $$\int_{S}\left(p n_{i}+\rho n_{j} u_{j} u_{i}\right) d S=0$$

  for the steady flow $\mathbf{u}=\left(u_{1}, u_{2}, u_{3}\right)$ and pressure $p$ of an inviscid,incompressible fluid of density $\rho$, where $S$ is a closed surface with normal $\mathbf{n}$.

  A cylindrical jet of water of area $A$ and speed $u$ impinges axisymmetrically on a stationary sphere of radius $a$ and is deflected into a conical sheet of vertex angle $\alpha$ as shown. Gravity is being ignored.

  

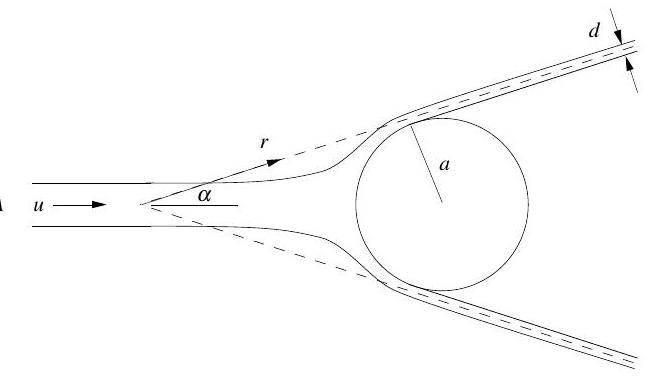
  Use a suitable form of Bernoulli's equation to determine the speed of the water in the conical sheet, being careful to state how the equation is being applied.

  Use conservation of mass to show that the width $d(r)$ of the sheet far from the point of impact is given by

  $$d=\frac{A}{2 \pi r \sin \alpha},$$

  where $r$ is the distance along the sheet measured from the vertex of the cone.

  Finally, use the momentum integral to determine the net force on the sphere in terms of $\rho, u, A$ and $\alpha$.

  comment

• 1.I.5E

  Fluid Dynamics

  Part IB, 2005

  Explain how a streamfunction $\psi$ can be used to represent in Cartesian Coordinates an incompressible flow in two dimensions. Show that the streamlines are given by $\psi=$ const.

  Consider the two-dimensional incompressible flow

  $$\mathbf{u}(x, y, t)=(x+\sin t,-y)$$

  (a) Find the streamfunction, and hence the streamlines at $t=\frac{\pi}{2}$.

  (b) Find the path of a fluid particle released at $t=0$ from $\left(x_{0}, 1\right)$. For what value of $x_{0}$ does the particle not tend to infinity?

  comment

• 1.II.17E

  Fluid Dynamics

  Part IB, 2005

  State Bernoulli's expression for the pressure in an unsteady potential flow with conservative force $-\nabla \chi$.

  A spherical bubble in an incompressible liquid of density $\rho$ has radius $R(t)$. If the pressure far from the bubble is $p_{\infty}$ and inside the bubble is $p_{b}$, show that

  $$p_{b}-p_{\infty}=\rho\left(\frac{3}{2} \dot{R}^{2}+R \ddot{R}\right)$$

  Calculate the kinetic energy $K(t)$ in the flow outside the bubble, and hence show that

  $$\dot{K}=\left(p_{b}-p_{\infty}\right) \dot{V}$$

  where $V(t)$ is the volume of the bubble.

  If $p_{b}(t)=p_{\infty} V_{0} / V$, show that

  $$K=K_{0}+p_{\infty}\left(V_{0} \ln \frac{V}{V_{0}}-V+V_{0}\right)$$

  where $K=K_{0}$ when $V=V_{0}$.

  comment

• 2.I.8E

  Fluid Dynamics

  Part IB, 2005

  For a steady flow of an incompressible fluid of density $\rho$, show that

  $$\mathbf{u} \times \boldsymbol{\omega}=\nabla H,$$

  where $\boldsymbol{\omega}=\nabla \times \mathbf{u}$ is the vorticity and $H$ is to be found. Deduce that $H$ is constant along streamlines.

  Now consider a flow in the $x y$-plane described by a streamfunction $\psi(x, y)$. Evaluate $\mathbf{u} \times \boldsymbol{\omega}$ and deduce from $H=H(\psi)$ that

  $$\frac{d H}{d \psi}+\omega=0$$

  comment

• 3.II.18E

  Fluid Dynamics

  Part IB, 2005

  Consider the velocity potential in plane polar coordinates

  $$\phi(r, \theta)=U\left(r+\frac{a^{2}}{r}\right) \cos \theta+\frac{\kappa \theta}{2 \pi}$$

  Find the velocity field and show that it corresponds to flow past a cylinder $r=a$ with circulation $\kappa$ and uniform flow $U$ at large distances.

  Find the distribution of pressure $p$ over the surface of the cylinder. Hence find the $x$ and $y$ components of the force on the cylinder

  $$\left(F_{x}, F_{y}\right)=\int(\cos \theta, \sin \theta) p a d \theta .$$

  comment

• 4.II.18E

  Fluid Dynamics

  Part IB, 2005

  A fluid of density $\rho_{1}$ occupies the region $z>0$ and a second fluid of density $\rho_{2}$ occupies the region $z<0$. State the equations and boundary conditions that are satisfied by the corresponding velocity potentials $\phi_{1}$ and $\phi_{2}$ and pressures $p_{1}$ and $p_{2}$ when the system is perturbed so that the interface is at $z=\zeta(x, t)$ and the motion is irrotational.

  Seek a set of linearised equations and boundary conditions when the disturbances are proportional to $e^{i(k x-\omega t)}$, and derive the dispersion relation

  $$\omega^{2}=\frac{\rho_{2}-\rho_{1}}{\rho_{2}+\rho_{1}} g k,$$

  where $g$ is the gravitational acceleration.

  comment

• 1.I.5A

  Fluid Dynamics

  Part IB, 2006

  Use the Euler equation for the motion of an inviscid fluid to derive the vorticity equation in the form

  $$D \boldsymbol{\omega} / D t=\boldsymbol{\omega} \cdot \nabla \mathbf{u} .$$

  Give a physical interpretation of the terms in this equation and deduce that irrotational flows remain irrotational.

  In a plane flow the vorticity at time $t=0$ has the uniform value $\boldsymbol{\omega}_{0} \neq \mathbf{0}$. Find the vorticity everywhere at times $t>0$.

  comment

• 1.II.17A

  Fluid Dynamics

  Part IB, 2006

  A point source of fluid of strength $m$ is located at $\mathbf{x}_{s}=(0,0, a)$ in inviscid fluid of density $\rho$. Gravity is negligible. The fluid is confined to the region $z \geqslant 0$ by the fixed boundary $z=0$. Write down the equation and boundary conditions satisfied by the velocity potential $\phi$. Find $\phi$.

  [Hint: consider the flow generated in unbounded fluid by the source $m$ together with an 'image source' of equal strength at $\overline{\mathbf{x}}_{s}=(0,0,-a)$.]

  Use Bernoulli's theorem, which may be stated without proof, to find the fluid pressure everywhere on $z=0$. Deduce the magnitude of the hydrodynamic force on the boundary $z=0$. Determine whether the boundary is attracted toward the source or repelled from it.

  comment

• 2.I.8A

  Fluid Dynamics

  Part IB, 2006

  Explain what is meant by a material time derivative, $D / D t$. Show that if the material velocity is $\mathbf{u}(\mathbf{x}, t)$ then

  $$D / D t=\partial / \partial t+\mathbf{u} \cdot \nabla$$

  When glass is processed in its liquid state, its temperature, $\theta(\mathbf{x}, t)$, satisfies the equation

  $$D \theta / D t=-\theta \text {. }$$

  The glass flows in a two-dimensional channel $-1<y<1, \quad x>0$ with steady velocity $\mathbf{u}=\left(1-y^{2}, 0\right)$. At $x=0$ the glass temperature is maintained at the constant value $\theta_{0}$. Find the steady temperature distribution throughout the channel.

  comment

• 3.II.18A

  Fluid Dynamics

  Part IB, 2006

  State and prove Bernoulli's theorem for a time-dependent irrotational flow of an inviscid fluid.

  A large vessel is part-filled with inviscid liquid of density $\rho$. The pressure in the air above the liquid is maintained at the constant value $P+p_{a}$, where $p_{a}$ is atmospheric pressure and $P>0$. Liquid can flow out of the vessel along a cylindrical tube of length $L$. The radius $a$ of the tube is much smaller than both $L$ and the linear dimensions of the vessel. Initially the tube is sealed and is full of liquid. At time $t=0$ the tube is opened and the liquid starts to flow. Assuming that the tube remains full of liquid, that the pressure at the open end of the tube is atmospheric and that $P$ is so large that gravity is negligible, determine the flux of liquid along the tube at time $t$.

  comment

• 4.II.18A

  Fluid Dynamics

  Part IB, 2006

  A rectangular tank has a horizontal base and vertical sides. Viewed from above, the cross-section of the tank is a square of side $a$. At rest, the depth of water in the tank is $h$. Suppose that the free-surface is disturbed in such a way that the flow in the water is irrotational. Take the pressure at the free surface as atmospheric. Starting from the appropriate non-linear expressions, obtain free-surface boundary conditions for the velocity potential appropriate for small-amplitude disturbances of the surface.

  Show that the governing equations and boundary conditions admit small-amplitude normal mode solutions for which the free-surface elevation above its equilibrium level is everywhere proportional to $e^{i \omega t}$, and find the frequencies, $\omega$, of such modes.

  comment

• 1.I.5D

  Fluid Dynamics

  Part IB, 2007

  A steady two-dimensional velocity field is given by

  $$\mathbf{u}(x, y)=(\alpha x-\beta y, \beta x-\alpha y), \quad \alpha>0, \quad \beta>0$$

  (i) Calculate the vorticity of the flow.

  (ii) Verify that $\mathbf{u}$ is a possible flow field for an incompressible fluid, and calculate the stream function.

  (iii) Show that the streamlines are bounded if and only if $\alpha<\beta$.

  (iv) What are the streamlines in the case $\alpha=\beta ?$

  comment

• 1.II.17D

  Fluid Dynamics

  Part IB, 2007

  Write down the Euler equation for the steady motion of an inviscid, incompressible fluid in a constant gravitational field. From this equation, derive (a) Bernoulli's equation and (b) the integral form of the momentum equation for a fixed control volume $V$ with surface $S$.

  (i) A circular jet of water is projected vertically upwards with speed $U_{0}$ from a nozzle of cross-sectional area $A_{0}$ at height $z=0$. Calculate how the speed $U$ and crosssectional area $A$ of the jet vary with $z$, for $z \ll U_{0}^{2} / 2 g$.

  (ii) A circular jet of speed $U$ and cross-sectional area $A$ impinges axisymmetrically on the vertex of a cone of semi-angle $\alpha$, spreading out to form an almost parallel-sided sheet on the surface. Choose a suitable control volume and, neglecting gravity, show that the force exerted by the jet on the cone is

  $$\rho A U^{2}(1-\cos \alpha)$$

  (iii) A cone of mass $M$ is supported, axisymmetrically and vertex down, by the jet of part (i), with its vertex at height $z=h$, where $h \ll U_{0}^{2} / 2 g$. Assuming that the result of part (ii) still holds, show that $h$ is given by

  $$\rho A_{0} U_{0}^{2}\left(1-\frac{2 g h}{U_{0}^{2}}\right)^{\frac{1}{2}}(1-\cos \alpha)=M g$$

  comment

• 2.I.8D

  Fluid Dynamics

  Part IB, 2007

  An incompressible, inviscid fluid occupies the region beneath the free surface $y=\eta(x, t)$ and moves with a velocity field given by the velocity potential $\phi(x, y, t)$; gravity acts in the $-y$ direction. Derive the kinematic and dynamic boundary conditions that must be satisfied by $\phi$ on $y=\eta(x, t)$.

  [You may assume Bernoulli's integral of the equation of motion:

  $$\left.\frac{p}{\rho}+\frac{\partial \phi}{\partial t}+\frac{1}{2}|\nabla \phi|^{2}+g y=F(t) .\right]$$

  In the absence of waves, the fluid has uniform velocity $U$ in the $x$ direction. Derive the linearised form of the above boundary conditions for small amplitude waves, and verify that they and Laplace's equation are satisfied by the velocity potential

  $$\phi=U x+\operatorname{Re}\left\{b e^{k y} e^{i(k x-\omega t)}\right\}$$

  where $|k b| \ll U$, with a corresponding expression for $\eta$, as long as

  $$(\omega-k U)^{2}=g k$$

  What are the propagation speeds of waves with a given wave-number $k ?$

  comment

• $3 . \mathrm{II} . 18 \mathrm{D}$

  Fluid Dynamics

  Part IB, 2007

  Given that the circulation round every closed material curve in an inviscid, incompressible fluid remains constant in time, show that the velocity field of such a fluid started from rest can be written as the gradient of a potential, $\phi$, that satisfies Laplace's equation.

  A rigid sphere of radius a moves in a straight line at speed $U$ in a fluid that is at rest at infinity. Using axisymmetric spherical polar coordinates $(r, \theta)$, with $\theta=0$ in the direction of motion, write down the boundary conditions on $\phi$ and, by looking for a solution of the form $\phi=f(r) \cos \theta$, show that the velocity potential is given by

  $$\phi=\frac{-U a^{3} \cos \theta}{2 r^{2}}$$

  Calculate the kinetic energy of the fluid.

  A rigid sphere of radius $a$ and uniform density $\rho_{b}$ is submerged in an infinite fluid of density $\rho$, under the action of gravity. Show that, when the sphere is released from rest, its initial upwards acceleration is

  $$\frac{2\left(\rho-\rho_{b}\right) g}{\rho+2 \rho_{b}}$$

  [Laplace's equation for an axisymmetric scalar field in spherical polars is:

  $$\left.\frac{1}{r^{2}} \frac{\partial}{\partial r}\left(r^{2} \frac{\partial \phi}{\partial r}\right)+\frac{1}{r^{2} \sin \theta} \frac{\partial}{\partial \theta}\left(\sin \theta \frac{\partial \phi}{\partial \theta}\right)=0 .\right]$$

  comment

• 4.II.18D

  Fluid Dynamics

  Part IB, 2007

  Starting from Euler's equation for an inviscid, incompressible fluid in the absence of body forces,

  $$\frac{\partial \mathbf{u}}{\partial t}+(\mathbf{u} . \nabla) \mathbf{u}=-\frac{1}{\rho} \nabla p$$

  derive the equation for the vorticity $\boldsymbol{\omega}=\nabla_{\wedge} \mathbf{u}$.

  [You may assume that $\left.\nabla_{\wedge}\left(\mathbf{a}_{\wedge} \mathbf{b}\right)=\mathbf{a} \nabla \cdot \mathbf{b}-\mathbf{b} \nabla \cdot \mathbf{a}+(\mathbf{b} . \nabla) \mathbf{a}-(\mathbf{a} . \nabla) \mathbf{b} .\right]$

  Show that, in a two-dimensional flow, vortex lines keep their strength and move with the fluid.

  Show that a two-dimensional flow driven by a line vortex of circulation $\Gamma$ at distance $b$ from a rigid plane wall is the same as if the wall were replaced by another vortex of circulation $-\Gamma$ at the image point, distance $b$ from the wall on the other side. Deduce that the first vortex will move at speed $\Gamma / 4 \pi b$ parallel to the wall.

  A line vortex of circulation $\Gamma$ moves in a quarter-plane, bounded by rigid plane walls at $x=0, y>0$ and $y=0, x>0$. Show that the vortex follows a trajectory whose equation in plane polar coordinates is $r \sin 2 \theta=$ constant.

  comment

• 1.I.5B

  Fluid Dynamics

  Part IB, 2008

  Verify that the two-dimensional flow given in Cartesian coordinates by

  $$\mathbf{u}=\left(\mathrm{e}^{y} \sinh x,-\mathrm{e}^{y} \cosh x\right)$$

  satisfies $\nabla \cdot \mathbf{u}=0$. Find the stream function $\psi(x, y)$. Sketch the streamlines.

  comment

• 1.II.17B

  Fluid Dynamics

  Part IB, 2008

  Two incompressible fluids flow in infinite horizontal streams, the plane of contact being $z=0$, with $z$ positive upwards. The flow is given by

  $$\mathbf{U}(\mathbf{r})= \begin{cases}U_{2} \hat{\mathbf{e}}_{x}, & z>0 \\ U_{1} \hat{\mathbf{e}}_{x}, & z<0\end{cases}$$

  where $\hat{\mathbf{e}}_{x}$ is the unit vector in the positive $x$ direction. The upper fluid has density $\rho_{2}$ and pressure $p_{0}-g \rho_{2} z$, the lower has density $\rho_{1}$ and pressure $p_{0}-g \rho_{1} z$, where $p_{0}$ is a constant and $g$ is the acceleration due to gravity.

  (i) Consider a perturbation to the flat surface $z=0$ of the form

  $$z \equiv \zeta(x, y, t)=\zeta_{0} e^{i(k x+\ell y)+s t} .$$

  State the kinematic boundary conditions on the velocity potentials $\phi_{i}$ that hold on the interface in the two domains, and show by linearising in $\zeta$ that they reduce to

  $$\frac{\partial \phi_{i}}{\partial z}=\frac{\partial \zeta}{\partial t}+U_{i} \frac{\partial \zeta}{\partial x} \quad(z=0, i=1,2) .$$

  (ii) State the dynamic boundary condition on the perturbed interface, and show by linearising in $\zeta$ that it reduces to

  $$\rho_{1}\left(U_{1} \frac{\partial \phi_{1}}{\partial x}+\frac{\partial \phi_{1}}{\partial t}+g \zeta\right)=\rho_{2}\left(U_{2} \frac{\partial \phi_{2}}{\partial x}+\frac{\partial \phi_{2}}{\partial t}+g \zeta\right) \quad(z=0)$$

  (iii) Use the velocity potentials

  $$\phi_{1}=U_{1} x+A_{1} e^{q z} e^{i(k x+\ell y)+s t}, \quad \phi_{2}=U_{2} x+A_{2} e^{-q z} e^{i(k x+\ell y)+s t},$$

  where $q=\sqrt{k^{2}+\ell^{2}}$, and the conditions in (i) and (ii) to perform a stability analysis. Show that the relation between $s, k$ and $\ell$ is

  $$s=-i k \frac{\rho_{1} U_{1}+\rho_{2} U_{2}}{\rho_{1}+\rho_{2}} \pm\left[\frac{k^{2} \rho_{1} \rho_{2}\left(U_{1}-U_{2}\right)^{2}}{\left(\rho_{1}+\rho_{2}\right)^{2}}-\frac{q g\left(\rho_{1}-\rho_{2}\right)}{\rho_{1}+\rho_{2}}\right]^{1 / 2} .$$

  Find the criterion for instability.

  comment

• 2.I.8B

  Fluid Dynamics

  Part IB, 2008

  (i) Show that for a two-dimensional incompressible flow $(u(x, y), v(x, y), 0)$, the vorticity is given by $\boldsymbol{\omega} \equiv \omega_{z} \hat{\mathbf{e}}_{z}=\left(0,0,-\nabla^{2} \psi\right)$ where $\psi$ is the stream function.

  (ii) Express the $z$-component of the vorticity equation

  $$\frac{\partial \boldsymbol{\omega}}{\partial t}+(\mathbf{u} \cdot \nabla) \boldsymbol{\omega}=(\boldsymbol{\omega} \cdot \nabla) \mathbf{u}$$

  in terms of the stream function $\psi$.

  comment

• 3.II.18B

  Fluid Dynamics

  Part IB, 2008

  An ideal liquid contained within a closed circular cylinder of radius $a$ rotates about the axis of the cylinder (assume this axis to be in the vertical $z$-direction).

  (i) Prove that the equation of continuity and the boundary conditions are satisfied by the velocity $\mathbf{v}=\boldsymbol{\Omega} \times \mathbf{r}$, where $\boldsymbol{\Omega}=\Omega \hat{\mathbf{e}}_{z}$ is the angular velocity, with $\hat{\mathbf{e}}_{z}$ the unit vector in the $z$-direction, which depends only on time, and $\mathbf{r}$ is the position vector measured from a point on the axis of rotation.

  (ii) Calculate the angular momentum $\mathbf{M}=\rho \int(\mathbf{r} \times \mathbf{v}) d V$ per unit length of the cylinder.

  (iii) Suppose the the liquid starts from rest and flows under the action of an external force per unit mass $\mathbf{f}=(\alpha x+\beta y, \gamma x+\delta y, 0)$. By taking the curl of the Euler equation, prove that

  $$\frac{d \Omega}{d t}=\frac{1}{2}(\gamma-\beta)$$

  (iv) Find the pressure.

  comment

• 4.II.18B

  Fluid Dynamics

  Part IB, 2008

  (i) Starting from Euler's equation for an incompressible fluid show that for potential flow with $\mathbf{u}=\nabla \phi$,

  $$\frac{\partial \phi}{\partial t}+\frac{1}{2} u^{2}+\chi=f(t)$$

  where $u=|\mathbf{u}|, \chi=p / \rho+V$, the body force per unit mass is $-\nabla V$ and $f(t)$ is an arbitrary function of time.

  (ii) Hence show that, for the steady flow of a liquid of density $\rho$ through a pipe of varying cross-section that is subject to a pressure difference $\Delta p=p_{1}-p_{2}$ between its two ends, the mass flow through the pipe per unit time is given by

  $$m \equiv \frac{d M}{d t}=S_{1} S_{2} \sqrt{\frac{2 \rho \Delta p}{S_{1}^{2}-S_{2}^{2}}}$$

  where $S_{1}$ and $S_{2}$ are the cross-sectional areas of the two ends.

  comment

• Paper 1, Section I, D

  Fluid Dynamics

  Part IB, 2009

  A steady velocity field $\mathbf{u}=\left(u_{r}, u_{\theta}, u_{z}\right)$ is given in cylindrical polar coordinates $(r, \theta, z)$ by

  $$u_{r}=-\alpha r, \quad u_{\theta}=\frac{\gamma}{r}\left(1-e^{-\beta r^{2}}\right), \quad u_{z}=2 \alpha z$$

  where $\alpha, \beta, \gamma$ are positive constants.

  Show that this represents a possible flow of an incompressible fluid, and find the vorticity $\omega$.

  Show further that

  $$\operatorname{curl}(\mathbf{u} \wedge \boldsymbol{\omega})=-\nu \nabla^{2} \boldsymbol{\omega}$$

  for a constant $\nu$ which should be calculated.

  [The divergence and curl operators in cylindrical polars are given by

  $$\begin{aligned} \operatorname{div} \mathbf{u} &=\frac{1}{r} \frac{\partial}{\partial r}\left(r u_{r}\right)+\frac{1}{r} \frac{\partial u_{\theta}}{\partial \theta}+\frac{\partial u_{z}}{\partial z} \\ \operatorname{curl} \mathbf{u} &=\left(\frac{1}{r} \frac{\partial u_{z}}{\partial \theta}-\frac{\partial u_{\theta}}{\partial z}, \frac{\partial u_{r}}{\partial z}-\frac{\partial u_{z}}{\partial r}, \frac{1}{r} \frac{\partial}{\partial r}\left(r u_{\theta}\right)-\frac{1}{r} \frac{\partial u_{r}}{\partial \theta}\right) \\ \text { and ,when } \boldsymbol{\omega} &=[0,0, \omega(r, z)], \\ \nabla^{2} \boldsymbol{\omega} &\left.=\left[0,0, \frac{1}{r} \frac{\partial}{\partial r}\left(r \frac{\partial \omega}{\partial r}\right)+\frac{\partial^{2} \omega}{\partial z^{2}}\right] .\right] \end{aligned}$$

  comment

• Paper 2, Section I, D

  Fluid Dynamics

  Part IB, 2009

  A fireman's hose full of water has cross-sectional area $A_{0}$, apart from a smooth contraction to the outlet nozzle which has cross-sectional area $A_{1}<A_{0}$. The volume flow rate of water through the hose is $Q$.

  Use Bernoulli's equation to calculate the pressure in the main part of the tube (relative to atmospheric pressure). Then use the integral momentum equation in the direction of the flow to show that the force $F$ that the fireman has to exert on the nozzle to keep it still is given by

  $$F=\frac{\rho Q^{2}}{2 A_{0}}\left(\frac{A_{0}}{A_{1}}-1\right)^{2}$$

  where $\rho$ is the density of water.

  comment

• Paper 1, Section II, D

  Fluid Dynamics

  Part IB, 2009

  A canal has uniform width and a bottom that is horizontal apart from a localised slowly-varying hump of height $D(x)$ whose maximum value is $D_{\text {max }}$. Far upstream the water has depth $h_{1}$ and velocity $u_{1}$. Show that the depth $h(x)$ of the water satisfies the following equation:

  $$\frac{D(x)}{h_{1}}=1-\frac{h}{h_{1}}-\frac{F}{2}\left(\frac{h_{1}^{2}}{h^{2}}-1\right)$$

  where $F=u_{1}^{2} / g h_{1}$.

  Describe qualitatively how $h(x)$ varies as the flow passes over the hump in the three cases

  $$\begin{array}{ll} \text { (i) } F<1 & \text { and } D_{\max }<D^{*} \\ \text { (ii) } F>1 & \text { and } D_{\max }<D^{*} \\ \text { (iii) } \quad D_{\max } & =D^{*}, \end{array}$$

  where $D^{*}=h_{1}\left(1-\frac{3}{2} F^{1 / 3}+\frac{1}{2} F\right)$.

  Calculate the water depth far downstream in case (iii) when $F<1$.

  comment

• Paper 3, Section II, D

  Fluid Dynamics

  Part IB, 2009

  Starting from Euler's equations for an inviscid incompressible fluid of density $\rho$ with no body force, undergoing irrotational motion, show that the pressure $p$ is given by

  $$\frac{p}{\rho}+\frac{\partial \phi}{\partial t}+\frac{1}{2}(\nabla \phi)^{2}=F(t)$$

  for some function $F(t)$, where $\phi$ is the velocity potential.

  The fluid occupies an infinite domain and contains a spherical gas bubble of radius $R(t)$ in which the pressure is $p_{g}$. The pressure in the fluid at infinity is $p_{\infty}$.

  Show that

  $$\ddot{R} R+\frac{3}{2} \dot{R}^{2}=\frac{p_{g}-p_{\infty}}{\rho}$$

  The bubble contains a fixed mass $M$ of gas in which

  $$p_{g}=C\left(M / R^{3}\right)^{2}$$

  for a constant $C$. At time $t=0, R=R_{0}, \dot{R}=0$ and $p_{g}=p_{\infty} / 2$. Show that

  $$\dot{R}^{2} R^{3}=\frac{p_{\infty}}{\rho}\left[R_{0}^{3}-\frac{R_{0}^{6}}{3 R^{3}}-\frac{2}{3} R^{3}\right]$$

  and deduce that the bubble radius oscillates between $R_{0}$ and $R_{0} / 2^{1 / 3}$.

  comment

• Paper 4, Section II, D

  Fluid Dynamics

  Part IB, 2009

  An inviscid incompressible fluid occupies a rectangular tank with vertical sides at $x=0, a$ and $y=0, b$ and a horizontal bottom at $z=-h$. The undisturbed free surface is at $z=0$.

  (i) Write down the equations and boundary conditions governing small amplitude free oscillations of the fluid, neglecting surface tension, and show that the frequencies $\omega$ of such oscillations are given by

  $$\frac{\omega^{2}}{g}=k \tanh k h, \text { where } k^{2}=\pi^{2}\left(\frac{m^{2}}{a^{2}}+\frac{n^{2}}{b^{2}}\right)$$

  for non-negative integers $m, n$, which cannot both be zero.

  (ii) The free surface is now acted on by a small external pressure

  $$p=\epsilon \rho g h \sin \Omega t \cos \frac{m \pi x}{a} \cos \frac{n \pi y}{b},$$

  where $\epsilon \ll 1$. Calculate the corresponding oscillation of the free surface when $\Omega$ is not equal to the quantity $\omega$ given by (1).

  Why does your solution break down as $\Omega \rightarrow \omega ?$

  comment

• Paper 1, Section I, B

  Fluid Dynamics

  Part IB, 2010

  A planar solenoidal velocity field has the velocity potential

  $$\phi(x, y, t)=x e^{-t}+y e^{t}$$

  Find and sketch (i) the streamlines at $t=0$; (ii) the pathline that passes through the origin at $t=0$; (iii) the locus at $t=0$ of points that pass through the origin at earlier times (streakline).

  comment

• Paper 2, Section I, B

  Fluid Dynamics

  Part IB, 2010

  Write down an expression for the velocity field of a line vortex of strength $\kappa$.

  Consider $N$ identical line vortices of strength $\kappa$ arranged at equal intervals round a circle of radius $a$. Show that the vortices all move around the circle at constant angular velocity $(N-1) \kappa /\left(4 \pi a^{2}\right)$.

  comment

• Paper 1, Section II, B

  Fluid Dynamics

  Part IB, 2010

  Starting with the Euler equations for an inviscid incompressible fluid, derive Bernoulli's theorem for unsteady irrotational flow.

  Inviscid fluid of density $\rho$ is contained within a U-shaped tube with the arms vertical, of height $h$ and with the same (unit) cross-section. The ends of the tube are closed. In the equilibrium state the pressures in the two arms are $p_{1}$ and $p_{2}$ and the heights of the fluid columns are $\ell_{1}, \ell_{2}$.

  The fluid in arm 1 is displaced upwards by a distance $\xi$ (and in the other arm downward by the same amount). In the subsequent evolution the pressure above each column may be taken as inversely proportional to the length of tube above the fluid surface. Using Bernoulli's theorem, show that $\xi(t)$ obeys the equation

  $$\rho\left(\ell_{1}+\ell_{2}\right) \ddot{\xi}+\frac{p_{1} \xi}{h-\ell_{1}-\xi}+\frac{p_{2} \xi}{h-\ell_{2}+\xi}+2 \rho g \xi=0$$

  Now consider the special case $\ell_{1}=\ell_{2}=\ell_{0}, p_{1}=p_{2}=p_{0}$. Construct a first integral of this equation and hence give an expression for the total kinetic energy $\rho \ell_{0} \dot{\xi}^{2}$ of the flow in terms of $\xi$ and the maximum displacement $\xi_{\max }$.

  comment

• Paper 3, Section II, B

  Fluid Dynamics

  Part IB, 2010

  Write down the exact kinematic and dynamic boundary conditions that apply at the free surface $z=\eta(x, t)$ of a fluid layer in the presence of gravity in the $z$-direction. Show how these may be approximated for small disturbances of a hydrostatic state about $z=0$. (The flow of the fluid is in the $(x, z)$-plane and may be taken to be irrotational, and the pressure at the free surface may be assumed to be constant.)

  Fluid of density $\rho$ fills the region $0>z>-h$. At $z=-h$ the $z$-component of the velocity is $\epsilon \operatorname{Re}\left(e^{i \omega t} \cos k x\right)$, where $|\epsilon| \ll 1$. Find the resulting disturbance of the free surface, assuming this to be small. Explain physically why your answer has a singularity for a particular value of $\omega^{2}$.

  comment

• Paper 4, Section II, B

  Fluid Dynamics

  Part IB, 2010

  Write down the velocity potential for a line source flow of strength $m$ located at $(r, \theta)=(d, 0)$ in polar coordinates $(r, \theta)$ and derive the velocity components $u_{r}, u_{\theta}$.

  A two-dimensional flow field consists of such a source in the presence of a circular cylinder of radius $a(a<d)$ centred at the origin. Show that the flow field outside the cylinder is the sum of the original source flow, together with that due to a source of the same strength at $\left(a^{2} / d, 0\right)$ and another at the origin, of a strength to be determined.

  Use Bernoulli's law to find the pressure distribution on the surface of the cylinder, and show that the total force exerted on it is in the $x$-direction and of magnitude

  $$\frac{m^{2} \rho}{2 \pi^{2}} \int_{0}^{2 \pi} \frac{a d^{2} \sin ^{2} \theta \cos \theta}{\left(a^{2}+d^{2}-2 a d \cos \theta\right)^{2}} d \theta$$

  where $\rho$ is the density of the fluid. Without evaluating the integral, show that it is positive. Comment on the fact that the force on the cylinder is therefore towards the source.

  comment

• Paper 1, Section I, B

  Fluid Dynamics

  Part IB, 2011

  Inviscid fluid is contained in a square vessel with sides of length $\pi L$ lying between $x=0, \pi L, y=0, \pi L$. The base of the container is at $z=-H$ where $H \gg L$ and the horizontal surface is at $z=0$ when the fluid is at rest. The variation of pressure of the air above the fluid may be neglected.

  Small amplitude surface waves are excited in the vessel.

  (i) Now let $H \rightarrow \infty$. Explain why on dimensional grounds the frequencies $\omega$ of such waves are of the form

  $$\omega=\left(\frac{\gamma g}{L}\right)^{\frac{1}{2}}$$

  for some positive dimensionless constants $\gamma$, where $g$ is the gravitational acceleration.

  It is given that the velocity potential $\phi$ is of the form

  $$\phi(x, y, z) \approx C \cos (m x / L) \cos (n y / L) \mathrm{e}^{\gamma z / L}$$

  where $m$ and $n$ are integers and $C$ is a constant.

  (ii) Why do cosines, rather than sines, appear in this expression?

  (iii) Give an expression for $\gamma$ in terms of $m$ and $n$.

  (iv) Give all possible values that $\gamma^{2}$ can take between 1 and 10 inclusive. How many different solutions for $\phi$ correspond to each of these values of $\gamma^{2} ?$

  comment

• Paper 2, Section I, D

  Fluid Dynamics

  Part IB, 2011

  A body of volume $V$ lies totally submerged in a motionless fluid of uniform density $\rho$. Show that the force $\mathbf{F}$ on the body is given by

  $$\mathbf{F}=-\int_{S}\left(p-p_{0}\right) \mathbf{n} d S$$

  where $p$ is the pressure in the fluid and $p_{0}$ is atmospheric pressure. You may use without proof the generalised divergence theorem in the form

  $$\int_{S} \phi \mathbf{n} d S=\int_{V} \boldsymbol{\nabla} \phi d V$$

  Deduce that

  $$\mathbf{F}=\rho g V \hat{\mathbf{z}},$$

  where $\hat{\mathbf{z}}$ is the vertically upward unit vector. Interpret this result.

  comment

• Paper 1, Section II, B

  Fluid Dynamics

  Part IB, 2011

  A spherical bubble in an incompressible fluid of density $\rho$ has radius $a(t)$. Write down an expression for the velocity field at a radius $R \geqslant a$.

  The pressure far from the bubble is $p_{\infty}$. What is the pressure at radius $R$ ?

  Find conditions on $a$ and its time derivatives that ensure that the maximum pressure in the fluid is reached at a radius $R_{\max }$ where $a<R_{\max }<\infty$. Give an expression for this maximum pressure when the conditions hold.

  Give the most general form of $a(t)$ that ensures that the pressure at $R=a(t)$ is $p_{\infty}$ for all time.

  comment

• Paper 3, Section II, $18 \mathrm{D}$

  Fluid Dynamics

  Part IB, 2011

  Water of constant density $\rho$ flows steadily through a long cylindrical tube, the wall of which is elastic. The exterior radius of the tube at a distance $z$ along the tube, $r(z)$, is determined by the pressure in the tube, $p(z)$, according to

  $$r(z)=r_{0}+b\left(p(z)-p_{0}\right)$$

  where $r_{0}$ and $p_{0}$ are the radius and pressure far upstream $(z \rightarrow-\infty)$, and $b$ is a positive constant.

  The interior radius of the tube is $r(z)-h(z)$, where $h(z)$, the thickness of the wall, is a given slowly varying function of $z$ which is zero at both ends of the pipe. The velocity of the water in the pipe is $u(z)$ and the water enters the pipe at velocity $V$.

  Show that $u(z)$ satisfies

  $$H=1-v^{-\frac{1}{2}}+\frac{1}{4} k\left(1-v^{2}\right)$$

  where $H=\frac{h}{r_{0}}, v=\frac{u}{V}$ and $k=\frac{2 b \rho V^{2}}{r_{0}}$. Sketch the graph of $H$ against $v$.

  Let $H_{m}$ be the maximum value of $H$ in the tube. Show that the flow is only possible if $H_{m}$ does not exceed a certain critical value $H_{c}$. Find $H_{c}$ in terms of $k$.

  Show that, under conditions to be determined (which include a condition on the value of $k)$, the water can leave the pipe with speed less than $V$.

  comment

• Paper 4, Section II, D

  Fluid Dynamics

  Part IB, 2011

  Show that an irrotational incompressible flow can be determined from a velocity potential $\phi$ that satisfies $\nabla^{2} \phi=0$.

  Given that the general solution of $\nabla^{2} \phi=0$ in plane polar coordinates is

  $$\phi=\sum_{n=-\infty}^{\infty}\left(a_{n} \cos n \theta+b_{n} \sin n \theta\right) r^{n}+c \log r+b \theta$$

  obtain the corresponding fluid velocity.

  A two-dimensional irrotational incompressible fluid flows past the circular disc with boundary $r=a$. For large $r$, the flow is uniform and parallel to the $x$-axis $(x=r \cos \theta)$. Write down the boundary conditions for large $r$ and on $r=a$, and hence derive the velocity potential in the form

  $$\phi=U\left(r+\frac{a^{2}}{r}\right) \cos \theta+\frac{\kappa \theta}{2 \pi}$$

  where $\kappa$ is the circulation.

  Show that the acceleration of the fluid at $r=a$ and $\theta=0$ is

  $$\frac{\kappa}{2 \pi a^{2}}\left(-\frac{\kappa}{2 \pi a} \mathbf{e}_{r}-2 U \mathbf{e}_{\theta}\right)$$

  comment

• Paper 1, Section I, A

  Fluid Dynamics

  Part IB, 2012

  Viscous fluid, with viscosity $\mu$ and density $\rho$ flows along a straight circular pipe of radius $R$. The average velocity of the flow is $U$. Define a Reynolds number for the flow.

  The flow is driven by a constant pressure gradient $-G>0$ along the pipe and the velocity is parallel to the axis of the pipe with magnitude $u(r)$ that satisfies

  $$\frac{\mu}{r} \frac{\mathrm{d}}{\mathrm{d} r}\left(r \frac{\mathrm{d} u}{\mathrm{~d} r}\right)=-G,$$

  where $r$ is the radial distance from the axis.

  State the boundary conditions on $u$ and find the velocity as a function of $r$ assuming that it is finite on the axis $r=0$. Hence, show that the shear stress $\tau$ at the pipe wall is independent of the viscosity. Why is this the case?

  comment

• Paper 2, Section I, A

  Fluid Dynamics

  Part IB, 2012

  Starting from Euler's equation for the motion of an inviscid fluid, derive the vorticity equation in the form

  $$\frac{D \boldsymbol{\omega}}{D t}=\boldsymbol{\omega} \cdot \nabla \boldsymbol{u}$$

  Deduce that an initially irrotational flow remains irrotational.

  Consider a plane flow that at time $t=0$ is described by the streamfunction

  $$\psi=x^{2}+y^{2} .$$

  Calculate the vorticity everywhere at times $t>0$.

  comment

• Paper 1, Section II, A

  Fluid Dynamics

  Part IB, 2012

  Consider inviscid, incompressible fluid flow confined to the $(x, y)$ plane. The fluid has density $\rho$, and gravity can be neglected. Using the conservation of volume flux, determine the velocity potential $\phi(r)$ of a point source of strength $m$, in terms of the distance $r$ from the source.

  Two point sources each of strength $m$ are located at $\boldsymbol{x}_{+}=(0, a)$ and $\boldsymbol{x}_{-}=(0,-a)$. Find the velocity potential of the flow.

  Show that the flow in the region $y \geqslant 0$ is equivalent to the flow due to a source at $\boldsymbol{x}_{+}$and a fixed boundary at $y=0 .$

  Find the pressure on the boundary $y=0$ and hence determine the force on the boundary.

  [Hint: you may find the substitution $x=a \tan \theta$ useful for the calculation of the pressure.]

  comment

• Paper 4, Section II, A

  Fluid Dynamics

  Part IB, 2012

  The equations governing the flow of a shallow layer of inviscid liquid of uniform depth $H$ rotating with angular velocity $\frac{1}{2} f$ about the vertical $z$-axis are

  $$\begin{aligned} \frac{\partial u}{\partial t}-f v &=-g \frac{\partial \eta}{\partial x} \\ \frac{\partial v}{\partial t}+f u &=-g \frac{\partial \eta}{\partial y} \\ \frac{\partial \eta}{t}+H\left(\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}\right) &=0 \end{aligned}$$

  where $u, v$ are the $x$ - and $y$-components of velocity, respectively, and $\eta$ is the elevation of the free surface. Show that these equations imply that

  $$\frac{\partial q}{\partial t}=0, \quad \text { where } \quad q=\omega-\frac{f \eta}{H} \text { and } \omega=\frac{\partial v}{\partial x}-\frac{\partial u}{\partial y}$$

  Consider an initial state where there is flow in the $y$-direction given by

  $$\begin{aligned} u &=\eta=0, \quad-\infty<x<\infty \\ v &= \begin{cases}\frac{g}{2 f} e^{2 x}, & x<0 \\ -\frac{g}{2 f} e^{-2 x}, & x>0\end{cases} \end{aligned}$$

  Find the initial potential vorticity.

  Show that when this initial state adjusts, there is a final steady state independent of $y$ in which $\eta$ satisfies

  $$\frac{\partial^{2} \eta}{\partial x^{2}}-\frac{\eta}{a^{2}}= \begin{cases}e^{2 x}, & x<0 \\ e^{-2 x}, & x>0\end{cases}$$

  where $a^{2}=g H / f^{2}$.

  In the case $a=1$, find the final free surface elevation that is finite at large $|x|$ and which is continuous and has continuous slope at $x=0$, and show that it is negative for all $x$.

  comment

• Paper 3, Section II, A

  Fluid Dynamics

  Part IB, 2012

  A rigid circular cylinder of radius $a$ executes small amplitude oscillations with velocity $U(t)$ in a direction perpendicular to its axis, while immersed in an inviscid fluid of density $\rho$ contained within a larger concentric fixed cylinder of radius $b$. Gravity is negligible. Neglecting terms quadratic in the amplitude, determine the boundary condition on the velocity on the inner cylinder, and calculate the velocity potential of the induced flow.

  With the same approximations show that the difference in pressures on the surfaces of the two cylinders has magnitude

  $$\rho \frac{\mathrm{d} U}{\mathrm{~d} t} \frac{a(b-a)}{b+a} \cos \theta$$

  where $\theta$ is the azimuthal angle measured from the direction of $U$.

  comment

• Paper 1, Section I, A

  Fluid Dynamics

  Part IB, 2013

  A two-dimensional flow is given by

  $$\mathbf{u}=(x,-y+t)$$

  Show that the flow is both irrotational and incompressible. Find a stream function $\psi(x, y)$ such that $\mathbf{u}=\left(\frac{\partial \psi}{\partial y},-\frac{\partial \psi}{\partial x}\right)$. Sketch the streamlines at $t=0$.

  Find the pathline of a fluid particle that passes through $\left(x_{0}, y_{0}\right)$ at $t=0$ in the form $y=f\left(x, x_{0}, y_{0}\right)$ and sketch the pathline for $x_{0}=1, y_{0}=1 .$

  comment

• Paper 2, Section I, A

  Fluid Dynamics

  Part IB, 2013

  An incompressible, inviscid fluid occupies the region beneath the free surface $y=\eta(x, t)$ and moves with a velocity field determined by the velocity potential $\phi(x, y, t) .$ Gravity acts in the $-y$ direction. You may assume Bernoulli's integral of the equation of motion:

  $$\frac{p}{\rho}+\frac{\partial \phi}{\partial t}+\frac{1}{2}|\nabla \phi|^{2}+g y=F(t)$$

  Give the kinematic and dynamic boundary conditions that must be satisfied by $\phi$ on $y=\eta(x, t)$.

  In the absence of waves, the fluid has constant uniform velocity $U$ in the $x$ direction. Derive the linearised form of the boundary conditions for small amplitude waves.

  Assume that the free surface and velocity potential are of the form:

  $$\begin{aligned} \eta &=a e^{i(k x-\omega t)} \\ \phi &=U x+i b e^{k y} e^{i(k x-\omega t)} \end{aligned}$$

  (where implicitly the real parts are taken). Show that

  $$(\omega-k U)^{2}=g k$$

  comment

• Paper 1, Section II, A

  Fluid Dynamics

  Part IB, 2013

  Starting from the Euler momentum equation, derive the form of Bernoulli's equation appropriate for an unsteady irrotational motion of an inviscid incompressible fluid.

  Water of density $\rho$ is driven through a horizontal tube of length $L$ and internal radius $a$ from a water-filled balloon attached to one end of the tube. Assume that the pressure exerted by the balloon is proportional to its current volume (in excess of atmospheric pressure). Also assume that water exits the tube at atmospheric pressure, and that gravity may be neglected. Show that the time for the balloon to empty does not depend on its initial volume. Find the maximum speed of water exiting the pipe.

  comment

• Paper 4, Section II, A

  Fluid Dynamics

  Part IB, 2013

  The axisymmetric, irrotational flow generated by a solid sphere of radius $a$ translating at velocity $U$ in an inviscid, incompressible fluid is represented by a velocity potential $\phi(r, \theta)$. Assume the fluid is at rest far away from the sphere. Explain briefly why $\nabla^{2} \phi=0$.

  By trying a solution of the form $\phi(r, \theta)=f(r) g(\theta)$, show that

  $$\phi=-\frac{U a^{3} \cos \theta}{2 r^{2}}$$

  and write down the fluid velocity.

  Show that the total kinetic energy of the fluid is $k M U^{2} / 4$ where $M$ is the mass of the sphere and $k$ is the ratio of the density of the fluid to the density of the sphere.

  A heavy sphere (i.e. $k<1$ ) is released from rest in an inviscid fluid. Determine its speed after it has fallen a distance $h$ in terms of $M, k, g$ and $h$.

  Note, in spherical polars:

  $$\begin{gathered} \boldsymbol{\nabla} \phi=\frac{\partial \phi}{\partial r} \mathbf{e}_{\mathbf{r}}+\frac{1}{r} \frac{\partial \phi}{\partial \theta} \mathbf{e}_{\theta} \\ \nabla^{2} \phi=\frac{1}{r^{2}} \frac{\partial}{\partial r}\left(r^{2} \frac{\partial \phi}{\partial r}\right)+\frac{1}{r^{2} \sin \theta} \frac{\partial}{\partial \theta}\left(\sin \theta \frac{\partial \phi}{\partial \theta}\right) \end{gathered}$$

  comment

• Paper 3, Section II, A

  Fluid Dynamics

  Part IB, 2013

  A layer of incompressible fluid of density $\rho$ and viscosity $\mu$ flows steadily down a plane inclined at an angle $\theta$ to the horizontal. The layer is of uniform thickness $h$ measured perpendicular to the plane and the viscosity of the overlying air can be neglected. Using coordinates $x$ parallel to the plane (in steepest downwards direction) and $y$ normal to the plane, write down the equations of motion and the boundary conditions on the plane and on the free top surface. Determine the pressure and velocity fields and show that the volume flux down the plane is

  $$\frac{\rho g h^{3} \sin \theta}{3 \mu}$$

  Consider now the case where a second layer of fluid, of uniform thickness $\alpha h$, viscosity $\beta \mu$ and density $\rho$, flows steadily on top of the first layer. Explain why one of the appropriate boundary conditions between the two fluids is

  $$\mu \frac{\partial}{\partial y} u\left(h_{-}\right)=\beta \mu \frac{\partial}{\partial y} u\left(h_{+}\right),$$

  where $u$ is the component of velocity in the $x$ direction and $h_{-}$and $h_{+}$refer to just below and just above the boundary respectively. Determine the velocity field in each layer.

  comment

• Paper 1, Section I, B

  Fluid Dynamics

  Part IB, 2014

  Constant density viscous fluid with dynamic viscosity $\mu$ flows in a two-dimensional horizontal channel of depth $h$. There is a constant pressure gradient $G>0$ in the horizontal $x$-direction. The upper horizontal boundary at $y=h$ is driven at constant horizontal speed $U>0$, with the lower boundary being held at rest. Show that the steady fluid velocity $u$ in the $x$-direction is

  $$u=\frac{-G}{2 \mu} y(h-y)+\frac{U y}{h}$$

  Show that it is possible to have $d u / d y<0$ at some point in the flow for sufficiently large pressure gradient. Derive a relationship between $G$ and $U$ so that there is no net volume flux along the channel. For the flow with no net volume flux, sketch the velocity profile.

  comment

• Paper 2, Section I, B

  Fluid Dynamics

  Part IB, 2014

  Consider the steady two-dimensional fluid velocity field

  $$\mathbf{u}=\left(\begin{array}{l} u \\ v \end{array}\right)=\left(\begin{array}{ll} \epsilon & -\gamma \\ \gamma & -\epsilon \end{array}\right)\left(\begin{array}{l} x \\ y \end{array}\right)$$

  where $\epsilon \geqslant 0$ and $\gamma \geqslant 0$. Show that the fluid is incompressible. The streamfunction $\psi$ is defined by $\mathbf{u}=\boldsymbol{\nabla} \times \boldsymbol{\Psi}$, where $\boldsymbol{\Psi}=(0,0, \psi)$. Show that $\psi$ is given by

  $$\psi=\epsilon x y-\frac{\gamma}{2}\left(x^{2}+y^{2}\right)$$

  Hence show that the streamlines are defined by

  $$(\epsilon-\gamma)(x+y)^{2}-(\epsilon+\gamma)(x-y)^{2}=C$$

  for $C$ a constant. For each of the three cases below, sketch the streamlines and briefly describe the flow. (i) $\epsilon=1, \gamma=0$, (ii) $\epsilon=0, \gamma=1$, (iii) $\epsilon=1, \gamma=1$.

  comment

• Paper 1, Section II, B

  Fluid Dynamics

  Part IB, 2014

  Consider the purely two-dimensional steady flow of an inviscid incompressible constant density fluid in the absence of body forces. For velocity $\mathbf{u}$, the vorticity is $\boldsymbol{\nabla} \times \mathbf{u}=\boldsymbol{\omega}=(0,0, \omega)$. Show that

  $$\mathbf{u} \times \boldsymbol{\omega}=\boldsymbol{\nabla}\left[\frac{p}{\rho}+\frac{1}{2}|\mathbf{u}|^{2}\right]$$

  where $p$ is the pressure and $\rho$ is the fluid density. Hence show that, if $\omega$ is a constant in both space and time,

  $$\frac{1}{2}|\mathbf{u}|^{2}+\omega \psi+\frac{p}{\rho}=C,$$

  where $C$ is a constant and $\psi$ is the streamfunction. Here, $\psi$ is defined by $\mathbf{u}=\boldsymbol{\nabla} \times \boldsymbol{\Psi}$, where $\boldsymbol{\Psi}=(0,0, \psi)$.

  Fluid in the annular region $a<r<2 a$ has constant (in both space and time) vorticity $\omega$. The streamlines are concentric circles, with the fluid speed zero on $r=2 a$ and $V>0$ on $r=a$. Calculate the velocity field, and hence show that

  $$\omega=\frac{-2 V}{3 a}$$

  Deduce that the pressure difference between the outer and inner edges of the annular region is

  $$\Delta p=\left(\frac{15-16 \ln 2}{18}\right) \rho V^{2}$$

  [Hint: Note that in cylindrical polar coordinates $(r, \phi, z)$, the curl of a vector field $\mathbf{A}(r, \phi)=[a(r, \phi), b(r, \phi), c(r, \phi)]$ is

  $$\boldsymbol{\nabla} \times \mathbf{A}=\left[\frac{1}{r} \frac{\partial c}{\partial \phi},-\frac{\partial c}{\partial r}, \frac{1}{r}\left(\frac{\partial(r b)}{\partial r}-\frac{\partial a}{\partial \phi}\right)\right]$$

  comment

• Paper 4, Section II, B

  Fluid Dynamics

  Part IB, 2014

  Consider a layer of fluid of constant density $\rho$ and equilibrium depth $h_{0}$ in a rotating frame of reference, rotating at constant angular velocity $\Omega$ about the vertical $z$-axis. The equations of motion are

  $$\begin{aligned} \frac{\partial u}{\partial t}-f v &=-\frac{1}{\rho} \frac{\partial p}{\partial x} \\ \frac{\partial v}{\partial t}+f u &=-\frac{1}{\rho} \frac{\partial p}{\partial y} \\ 0 &=-\frac{\partial p}{\partial z}-\rho g \end{aligned}$$

  where $p$ is the fluid pressure, $u$ and $v$ are the fluid velocities in the $x$-direction and $y$ direction respectively, $f=2 \Omega$, and $g$ is the constant acceleration due to gravity. You may also assume that the horizontal extent of the layer is sufficiently large so that the layer may be considered to be shallow, such that vertical velocities may be neglected.

  By considering mass conservation, show that the depth $h(x, y, t)$ of the layer satisfies

  $$\frac{\partial h}{\partial t}+\frac{\partial}{\partial x}(h u)+\frac{\partial}{\partial y}(h v)=0 .$$

  Now assume that $h=h_{0}+\eta(x, y, t)$, where $|\eta| \ll h_{0}$. Show that the (linearised) potential vorticity $\mathbf{Q}=Q \hat{\mathbf{z}}$, defined by

  $$Q=\zeta-\eta \frac{f}{h_{0}}, \text { where } \zeta=\frac{\partial v}{\partial x}-\frac{\partial u}{\partial y}$$

  and $\hat{\mathbf{z}}$ is the unit vector in the vertical $z$-direction, is a constant in time, i.e. $Q=Q_{0}(x, y)$.

  When $Q_{0}=0$ everywhere, establish that the surface perturbation $\eta$ satisfies

  $$\frac{\partial^{2} \eta}{\partial t^{2}}-g h_{0}\left(\frac{\partial^{2} \eta}{\partial x^{2}}+\frac{\partial^{2} \eta}{\partial y^{2}}\right)+f^{2} \eta=0$$

  and show that this equation has wave-like solutions $\eta=\eta_{0} \cos [k(x-c t)]$ when $c$ and $k$ are related through a dispersion relation to be determined. Show that, to leading order, the trajectories of fluid particles for these waves are ellipses. Assuming that $\eta_{0}>0, k>0$, $c>0$ and $f>0$, sketch the fluid velocity when $k(x-c t)=n \pi / 2$ for $n=0,1,2,3$.

  comment

• Paper 3, Section II, B

  Fluid Dynamics

  Part IB, 2014

  A bubble of gas occupies the spherical region $r \leqslant R(t)$, and an incompressible irrotational liquid of constant density $\rho$ occupies the outer region $r \geqslant R$, such that as $r \rightarrow \infty$ the liquid is at rest with constant pressure $p_{\infty}$. Briefly explain why it is appropriate to use a velocity potential $\phi(r, t)$ to describe the liquid velocity u.

  By applying continuity of velocity across the gas-liquid interface, show that the liquid pressure (for $r \geqslant R$ ) satisfies

  $$\frac{p}{\rho}+\frac{1}{2}\left(\frac{R^{2} \dot{R}}{r^{2}}\right)^{2}-\frac{1}{r} \frac{d}{d t}\left(R^{2} \dot{R}\right)=\frac{p_{\infty}}{\rho}, \quad \text { where } \dot{R}=\frac{d R}{d t} .$$

  Show that the excess pressure $p_{s}-p_{\infty}$ at the bubble surface $r=R$ is

  $$p_{s}-p_{\infty}=\frac{\rho}{2}\left(3 \dot{R}^{2}+2 R \ddot{R}\right), \quad \text { where } \ddot{R}=\frac{d^{2} R}{d t^{2}}$$

  and hence that

  $$p_{s}-p_{\infty}=\frac{\rho}{2 R^{2}} \frac{d}{d R}\left(R^{3} \dot{R}^{2}\right)$$

  The pressure $p_{g}(t)$ inside the gas bubble satisfies the equation of state

  $$p_{g} V^{4 / 3}=C$$

  where $C$ is a constant, and $V(t)$ is the bubble volume. At time $t=0$ the bubble is at rest with radius $R=a$. If the bubble then expands and comes to rest at $R=2 a$, determine the required gas pressure $p_{0}$ at $t=0$ in terms of $p_{\infty}$.

  [You may assume that there is contact between liquid and gas for all time, that all motion is spherically symmetric about the origin $r=0$, and that there is no body force. You may also assume Bernoulli's integral of the equation of motion to determine the liquid pressure

  $$\frac{p}{\rho}+\frac{\partial \phi}{\partial t}+\frac{1}{2}|\nabla \phi|^{2}=A(t)$$

  where $\phi(r, t)$ is the velocity potential.]

  comment

• Paper 1, Section I, B

  Fluid Dynamics

  Part IB, 2015

  Consider a spherical bubble of radius $a$ in an inviscid fluid in the absence of gravity. The flow at infinity is at rest and the bubble undergoes translation with velocity $\mathbf{U}=U(t) \hat{\mathbf{x}}$. We assume that the flow is irrotational and derives from a potential given in spherical coordinates by

  $$\phi(r, \theta)=U(t) \frac{a^{3}}{2 r^{2}} \cos \theta,$$

  where $\theta$ is measured with respect to $\hat{\mathbf{x}}$. Compute the force, $\mathbf{F}$, acting on the bubble. Show that the formula for $\mathbf{F}$ can be interpreted as the acceleration force of a fraction $\alpha<1$ of the fluid displaced by the bubble, and determine the value of $\alpha$.

  comment

• Paper 2, Section I, B

  Fluid Dynamics

  Part IB, 2015

  Consider the two-dimensional velocity field $\mathbf{u}=(u, v)$ with

  $$u(x, y)=x^{2}-y^{2}, \quad v(x, y)=-2 x y$$

  (i) Show that the flow is incompressible and irrotational.

  (ii) Derive the velocity potential, $\phi$, and the streamfunction, $\psi$.

  (iii) Plot all streamlines passing through the origin.

  (iv) Show that the complex function $w=\phi+i \psi$ (where $i^{2}=-1$ ) can be written solely as a function of the complex coordinate $z=x+i y$ and determine that function.

  comment

• Paper 1, Section II, B

  Fluid Dynamics

  Part IB, 2015

  A fluid layer of depth $h_{1}$ and dynamic viscosity $\mu_{1}$ is located underneath a fluid layer of depth $h_{2}$ and dynamic viscosity $\mu_{2}$. The total fluid system of depth $h=h_{1}+h_{2}$ is positioned between a stationary rigid plate at $y=0$ and a rigid plate at $y=h$ moving with speed $\mathbf{U}=U \hat{\mathbf{x}}$, where $U$ is constant. Ignore the effects of gravity.

  (i) Using dimensional analysis only, and the fact that the stress should be linear in $U$, derive the expected form of the shear stress acted by the fluid on the plate at $y=0$ as a function of $U, h_{1}, h_{2}, \mu_{1}$ and $\mu_{2}$.

  (ii) Solve for the unidirectional velocity profile between the two plates. State clearly all boundary conditions you are using to solve this problem.

  (iii) Compute the exact value of the shear stress acted by the fluid on the plate at $y=0$. Compare with the results in (i).

  (iv) What is the condition on the viscosity of the bottom layer, $\mu_{1}$, for the stress in (iii) to be smaller than it would be if the fluid had constant viscosity $\mu_{2}$ in both layers?

  (v) Show that the stress acting on the plate at $y=h$ is equal and opposite to the stress on the plate at $y=0$ and justify this result physically.

  comment

• Paper 4, Section II, B

  Fluid Dynamics

  Part IB, 2015

  Consider a steady inviscid, incompressible fluid of constant density $\rho$ in the absence of external body forces. A cylindrical jet of area $A$ and speed $U$ impinges fully on a stationary sphere of radius $R$ with $A<\pi R^{2}$. The flow is assumed to remain axisymmetric and be deflected into a conical sheet of vertex angle $\alpha>0$.

  (i) Show that the speed of the fluid in the conical sheet is constant.

  (ii) Use conservation of mass to show that the width $d(r)$ of the fluid sheet at a distance $r \gg R$ from point of impact is given by

  $$d(r)=\frac{A}{2 \pi r \sin \alpha}$$

  (iii) Use Euler's equation to derive the momentum integral equation

  $$\iint_{S}\left(p n_{i}+\rho n_{j} u_{j} u_{i}\right) d S=0$$

  for a closed surface $S$ with normal $\mathbf{n}$ where $u_{m}$ is the $m$ th component of the velocity field in cartesian coordinates and $p$ is the pressure.

  (iv) Use the result from (iii) to calculate the net force on the sphere.

  comment

• Paper 3, Section II, B

  Fluid Dynamics

  Part IB, 2015

  A source of sound induces a travelling wave of pressure above the free surface of a fluid located in the $z<0$ domain as

  $$p=p_{a t m}+p_{0} \cos (k x-\omega t),$$

  with $p_{0} \ll p_{a t m}$. Here $k$ and $\omega$ are fixed real numbers. We assume that the flow induced in the fluid is irrotational.

  (i) State the linearized equation of motion for the fluid and the free surface, $z=h(x, t)$, with all boundary conditions.

  (ii) Solve for the velocity potential, $\phi(x, z, t)$, and the height of the free surface, $h(x, t)$. Verify that your solutions are dimensionally correct.

  (iii) Interpret physically the behaviour of the solution when $\omega^{2}=g k$.

  comment

• Paper 1, Section I, C

  Fluid Dynamics

  Part IB, 2016

  Consider the flow field in cartesian coordinates $(x, y, z)$ given by

  $$\mathbf{u}=\left(-\frac{A y}{x^{2}+y^{2}}, \frac{A x}{x^{2}+y^{2}}, U(z)\right)$$

  where $A$ is a constant. Let $\mathcal{D}$ denote the whole of $\mathbb{R}^{3}$ excluding the $z$ axis.

  (a) Determine the conditions on $A$ and $U(z)$ for the flow to be both incompressible and irrotational in $\mathcal{D}$.

  (b) Calculate the circulation along any closed curve enclosing the $z$ axis.

  comment

• Paper 2, Section I, C

  Fluid Dynamics

  Part IB, 2016

  A steady, two-dimensional unidirectional flow of a fluid with dynamic viscosity $\mu$ is set up between two plates at $y=0$ and $y=h$. The plate at $y=0$ is stationary while the plate at $y=h$ moves with constant speed $U \mathbf{e}_{x}$. The fluid is also subject to a constant pressure gradient $-G \mathbf{e}_{x}$. You may assume that the fluid velocity $\mathbf{u}$ has the form $\mathbf{u}=u(y) \mathbf{e}_{x}$.

  (a) State the equation satisfied by $u(y)$ and its boundary conditions.

  (b) Calculate $u(y)$.

  (c) Show that the value of $U$ may be chosen to lead to zero viscous shear stress acting on the bottom plate and calculate the resulting flow rate.

  comment

• Paper 1, Section II, $17 \mathrm{C}$

  Fluid Dynamics

  Part IB, 2016

  (a) For a velocity field $\mathbf{u}$, show that $\mathbf{u} \cdot \boldsymbol{\nabla} \mathbf{u}=\boldsymbol{\nabla}\left(\frac{1}{2} \mathbf{u}^{2}\right)-\mathbf{u} \times \boldsymbol{\omega}$, where $\boldsymbol{\omega}$ is the flow vorticity.

  (b) For a scalar field $H(\mathbf{r})$, show that if $\mathbf{u} \cdot \nabla H=0$, then $H$ is constant along the flow streamlines.

  (c) State the Euler equations satisfied by an inviscid fluid of constant density subject to conservative body forces.

  (i) If the flow is irrotational, show that an exact first integral of the Euler equations may be obtained.

  (ii) If the flow is not irrotational, show that although an exact first integral of the Euler equations may not be obtained, a similar quantity is constant along the flow streamlines provided the flow is steady.

  (iii) If the flow is now in a frame rotating with steady angular velocity $\Omega \mathbf{e}_{z}$, establish that a similar quantity is constant along the flow streamlines with an extra term due to the centrifugal force when the flow is steady.

  comment

• Paper 4, Section II, C

  Fluid Dynamics

  Part IB, 2016

  (a) Show that for an incompressible fluid, $\nabla \times \boldsymbol{\omega}=-\nabla^{2} \mathbf{u}$, where $\boldsymbol{\omega}$ is the flow vorticity,

  (b) State the equation of motion for an inviscid flow of constant density in a rotating frame subject to gravity. Show that, on Earth, the local vertical component of the centrifugal force is small compared to gravity. Present a scaling argument to justify the linearisation of the Euler equations for sufficiently large rotation rates, and hence deduce the linearised version of the Euler equations in a rapidly rotating frame.

  (c) Denoting the rotation rate of the frame as $\boldsymbol{\Omega}=\Omega \mathbf{e}_{z}$, show that the linearised Euler equations may be manipulated to obtain an equation for the velocity field $\mathbf{u}$ in the form

  $$\frac{\partial^{2} \nabla^{2} \mathbf{u}}{\partial t^{2}}+4 \Omega^{2} \frac{\partial^{2} \mathbf{u}}{\partial z^{2}}=\mathbf{0}$$

  (d) Assume that there exist solutions of the form $\mathbf{u}=\mathbf{U}_{0} \exp [i(\mathbf{k} \cdot \mathbf{x}-\omega t)]$. Show that $\omega=\pm 2 \Omega \cos \theta$ where the angle $\theta$ is to be determined.

  comment

• Paper 3, Section II, C

  Fluid Dynamics

  Part IB, 2016

  A layer of thickness $h_{1}$ of a fluid of density $\rho_{1}$ is located above a layer of thickness $h_{2}$ of a fluid of density $\rho_{2}>\rho_{1}$. The two-fluid system is bounded by two impenetrable surfaces at $y=h_{1}$ and $y=-h_{2}$ and is assumed to be two-dimensional (i.e. independent of $z$ ). The fluid is subsequently perturbed, and the interface between the two fluids is denoted $y=\eta(x, t)$.

  (a) Assuming irrotational motion in each fluid, state the equations and boundary conditions satisfied by the flow potentials, $\varphi_{1}$ and $\varphi_{2}$.

  (b) The interface is perturbed by small-amplitude waves of the form $\eta=\eta_{0} e^{i(k x-\omega t)}$, with $\eta_{0} k \ll 1$. State the equations and boundary conditions satisfied by the linearised system.

  (c) Calculate the dispersion relation of the waves relating the frequency $\omega$ to the wavenumber $k$.

  comment

• Paper 1, Section I, D

  Fluid Dynamics

  Part IB, 2017

  For each of the flows

  (i) $\mathbf{u}=\left(2 x y, x^{2}+y^{2}\right)$

  (ii) $\mathbf{u}=(-2 y,-2 x)$

  determine whether or not the flow is incompressible and/or irrotational. Find the associated velocity potential and/or stream function when appropriate. For either one of the flows, sketch the streamlines of the flow, indicating the direction of the flow.

  comment

• Paper 2, Section I, $7 \mathrm{D}$

  Fluid Dynamics

  Part IB, 2017

  From Euler's equations describing steady inviscid fluid flow under the action of a conservative force, derive Bernoulli's equation for the pressure along a streamline of the flow, defining all variables that you introduce.

  Water fills an inverted, open, circular cone (radius increasing upwards) of half angle $\pi / 4$ to a height $h_{0}$ above its apex. At time $t=0$, the tip of the cone is removed to leave a small hole of radius $\epsilon \ll h_{0}$. Assuming that the flow is approximately steady while the depth of water $h(t)$ is much larger than $\epsilon$, show that the time taken for the water to drain is approximately

  $$\left(\frac{2}{25} \frac{h_{0}^{5}}{\epsilon^{4} g}\right)^{1 / 2}$$

  comment

• Paper 1, Section II, D

  Fluid Dynamics

  Part IB, 2017

  A layer of thickness $h$ of fluid of density $\rho$ and dynamic viscosity $\mu$ flows steadily down and parallel to a rigid plane inclined at angle $\alpha$ to the horizontal. Wind blows over the surface of the fluid and exerts a stress $S$ on the surface of the fluid in the upslope direction.

  (a) Draw a diagram of this situation, including indications of the applied stresses and body forces, a suitable coordinate system and a representation of the expected velocity profile.

  (b) Write down the equations and boundary conditions governing the flow, with a brief description of each, paying careful attention to signs. Solve these equations to determine the pressure and velocity fields.

  (c) Determine the volume flux and show that there is no net flux if

  $$S=\frac{2}{3} \rho g h \sin \alpha$$

  Draw a sketch of the corresponding velocity profile.

  (d) Determine the value of $S$ for which the shear stress on the rigid plane is zero and draw a sketch of the corresponding velocity profile.

  comment

• Paper 4, Section II, D

  Fluid Dynamics

  Part IB, 2017

  The linearised equations governing the horizontal components of flow $\mathbf{u}(x, y, t)$ in a rapidly rotating shallow layer of depth $h=h_{0}+\eta(x, y, t)$, where $\eta \ll h_{0}$, are

  $$\begin{gathered} \frac{\partial \mathbf{u}}{\partial t}+\mathbf{f} \times \mathbf{u}=-g \nabla \eta \\ \frac{\partial \eta}{\partial t}+h_{0} \nabla \cdot \mathbf{u}=0 \end{gathered}$$

  where $\mathbf{f}=f \mathbf{e}_{z}$ is the constant Coriolis parameter, and $\mathbf{e}_{z}$ is the unit vector in the vertical direction.

  Use these equations, either in vector form or using Cartesian components, to show that the potential vorticity

  $$\mathbf{Q}=\zeta-\frac{\eta}{h_{0}} \mathbf{f}$$

  is independent of time, where $\zeta=\nabla \times \mathbf{u}$ is the relative vorticity.

  Derive the equation

  $$\frac{\partial^{2} \eta}{\partial t^{2}}-g h_{0} \nabla^{2} \eta+f^{2} \eta=-h_{0} \mathbf{f} \cdot \mathbf{Q}$$

  In the case that $\mathbf{Q} \equiv 0$, determine and sketch the dispersion relation $\omega(k)$ for plane waves with $\eta=A e^{i(k x+\omega t)}$, where $A$ is constant. Discuss the nature of the waves qualitatively: do long waves propagate faster or slower than short waves; how does the phase speed depend on wavelength; does rotation have more effect on long waves or short waves; how dispersive are the waves?

  comment

• Paper 3, Section II, D

  Fluid Dynamics

  Part IB, 2017

  Use Euler's equations to derive the vorticity equation

  $$\frac{D \boldsymbol{\omega}}{D t}=\boldsymbol{\omega} \cdot \nabla \mathbf{u}$$

  where $\mathbf{u}$ is the fluid velocity and $\boldsymbol{\omega}$ is the vorticity.

  Consider axisymmetric, incompressible, inviscid flow between two rigid plates at $z=h(t)$ and $z=-h(t)$ in cylindrical polar coordinates $(r, \theta, z)$, where $t$ is time. Using mass conservation, or otherwise, find the complete flow field whose radial component is independent of $z$.

  Now suppose that the flow has angular velocity $\boldsymbol{\Omega}=\Omega(t) \mathbf{e}_{z}$ and that $\Omega=\Omega_{0}$ when $h=h_{0}$. Use the vorticity equation to determine the angular velocity for subsequent times as a function of $h$. What physical principle does your result illustrate?

  comment

• Paper 1, Section I, D

  Fluid Dynamics

  Part IB, 2018

  Show that the flow with velocity potential

  $$\phi=\frac{q}{2 \pi} \ln r$$

  in two-dimensional, plane-polar coordinates $(r, \theta)$ is incompressible in $r>0$. Determine the flux of fluid across a closed contour $C$ that encloses the origin. What does this flow represent?

  Show that the flow with velocity potential

  $$\phi=\frac{q}{4 \pi} \ln \left(x^{2}+(y-a)^{2}\right)+\frac{q}{4 \pi} \ln \left(x^{2}+(y+a)^{2}\right)$$

  has no normal flow across the line $y=0$. What fluid flow does this represent in the unbounded plane? What flow does it represent for fluid occupying the domain $y>0$ ?

  comment

• Paper 2, Section I, D

  Fluid Dynamics

  Part IB, 2018

  The Euler equations for steady fluid flow $\mathbf{u}$ in a rapidly rotating system can be written

  $$\rho \mathbf{f} \times \mathbf{u}=-\nabla p+\rho \mathbf{g},$$

  where $\rho$ is the density of the fluid, $p$ is its pressure, $\mathbf{g}$ is the acceleration due to gravity and $\mathbf{f}=(0,0, f)$ is the constant Coriolis parameter in a Cartesian frame of reference $(x, y, z)$, with $z$ pointing vertically upwards.

  Fluid occupies a layer of slowly-varying height $h(x, y)$. Given that the pressure $p=p_{0}$ is constant at $z=h$ and that the flow is approximately horizontal with components $\mathbf{u}=(u, v, 0)$, show that the contours of $h$ are streamlines of the horizontal flow. What is the leading-order horizontal volume flux of fluid between two locations at which $h=h_{0}$ and $h=h_{0}+\Delta h$, where $\Delta h \ll h_{0}$ ?

  Identify the dimensions of all the quantities involved in your expression for the volume flux and show that your expression is dimensionally consistent.

  comment

• Paper 1, Section II, D

  Fluid Dynamics

  Part IB, 2018

  A layer of fluid of dynamic viscosity $\mu$, density $\rho$ and uniform thickness $h$ flows down a rigid vertical plane. The adjacent air has uniform pressure $p_{0}$ and exerts a tangential stress on the fluid that is proportional to the surface velocity and opposes the flow, with constant of proportionality $k$. The acceleration due to gravity is $g$.

  (a) Draw a diagram of this situation, including indications of the applied stresses and body forces, a suitable coordinate system and a representation of the expected velocity profile.

  (b) Write down the equations and boundary conditions governing the flow, with a brief description of each, paying careful attention to signs. Solve these equations to determine the pressure and velocity fields in terms of the parameters given above.

  (c) Show that the surface velocity of the fluid layer is $\frac{\rho g h^{2}}{2 \mu}\left(1+\frac{k h}{\mu}\right)^{-1}$.

  (d) Determine the volume flux per unit width of the plane for general values of $k$ and its limiting values when $k \rightarrow 0$ and $k \rightarrow \infty$.

  comment

• Paper 4, Section II, D

  Fluid Dynamics

  Part IB, 2018

  A deep layer of inviscid fluid is initially confined to the region $0<x<a, 0<y<a$, $z<0$ in Cartesian coordinates, with $z$ directed vertically upwards. An irrotational disturbance is caused to the fluid so that its upper surface takes position $z=\eta(x, y, t)$. Determine the linear normal modes of the system and the dispersion relation between the frequencies of the normal modes and their wavenumbers.

  If the interface is initially displaced to position $z=\epsilon \cos \frac{3 \pi x}{a} \cos \frac{4 \pi y}{a}$ and released from rest, where $\epsilon$ is a small constant, determine its position for subsequent times. How far below the surface will the velocity have decayed to $1 / e$ times its surface value?

  comment

• Paper 3, Section II, D

  Fluid Dynamics

  Part IB, 2018

  A soap bubble of radius $a(t)$ is attached to the end of a long, narrow straw of internal radius $\epsilon$ and length $L$, the other end of which is open to the atmosphere. The pressure difference between the inside and outside of the bubble is $2 \gamma / a$, where $\gamma$ is the surface tension of the soap bubble. At time $t=0, a=a_{0}$ and the air in the straw is at rest. Assume that the flow of air through the straw is irrotational and consider the pressure drop along the straw to show that subsequently

  $$a^{3} \ddot{a}+2 a^{2} \dot{a}^{2}=-\frac{\gamma \epsilon^{2}}{2 \rho L},$$

  where $\rho$ is the density of air.

  By multiplying the equation by $2 a \dot{a}$ and integrating, or otherwise, determine an implicit equation for $a(t)$ and show that the bubble disappears in a time

  $$t=\frac{\pi}{2} \frac{a_{0}^{2}}{\epsilon}\left(\frac{\rho L}{2 \gamma}\right)^{1 / 2}$$

  [Hint: The substitution $a=a_{0} \sin \theta$ can be used.]

  comment

• Paper 1, Section I, C

  Fluid Dynamics

  Part IB, 2019

  A viscous fluid flows steadily down a plane that is inclined at an angle $\alpha$ to the horizontal. The fluid layer is of uniform thickness and has a free upper surface. Determine the velocity profile in the direction perpendicular to the plane and also the volume flux (per unit width), in terms of the gravitational acceleration $g$, the angle $\alpha$, the kinematic viscosity $\nu$ and the thickness $h$ of the fluid layer.

  Show that the volume flux is reduced if the free upper surface is replaced by a stationary plane boundary, and give a physical explanation for this.

  comment

• Paper 2, Section I, C

  Fluid Dynamics

  Part IB, 2019

  Consider the steady flow

  $$u_{x}=\sin x \cos y, \quad u_{y}=-\cos x \sin y, \quad u_{z}=0$$

  where $(x, y, z)$ are Cartesian coordinates. Show that $\boldsymbol{\nabla} \cdot \mathbf{u}=0$ and determine the streamfunction. Calculate the vorticity and verify that the vorticity equation is satisfied in the absence of viscosity. Sketch the streamlines in the region $0<x<2 \pi, 0<y<2 \pi$.

  comment

• Paper 1, Section II, C

  Fluid Dynamics

  Part IB, 2019

  Explain why the irrotational flow of an incompressible fluid can be expressed in terms of a velocity potential $\phi$ that satisfies Laplace's equation.

  The axis of a stationary cylinder of radius $a$ coincides with the $z$-axis of a Cartesian coordinate system $(x, y, z)$ with unit vectors $\left(\mathbf{e}_{x}, \mathbf{e}_{y}, \mathbf{e}_{z}\right)$. A fluid of density $\rho$ flows steadily past the cylinder such that the velocity field $\mathbf{u}$ is independent of $z$ and has no component in the $z$-direction. The flow is irrotational but there is a constant non-zero circulation

  $$\oint \mathbf{u} \cdot d \mathbf{r}=\kappa$$

  around every closed curve that encloses the cylinder once in a positive sense. Far from the cylinder, the velocity field tends towards the uniform flow $\mathbf{u}=U \mathbf{e}_{x}$, where $U$ is a constant.

  State the boundary conditions on the velocity potential, in terms of polar coordinates $(r, \theta)$ in the $(x, y)$-plane. Explain why the velocity potential is not required to be a single-valued function of position. Hence obtain the appropriate solution $\phi(r, \theta)$, in terms of $a, U$ and $\kappa$.

  Neglecting gravity, show that the net force on the cylinder, per unit length in the $z$-direction, is

  $$-\rho \kappa U \mathbf{e}_{y}$$

  Determine the number and location of stagnation points in the flow as a function of the dimensionless parameter

  $$\lambda=\frac{\kappa}{4 \pi U a}$$

  comment

• Paper 4, Section II, C

  Fluid Dynamics

  Part IB, 2019

  The linear shallow-water equations governing the motion of a fluid layer in the neighbourhood of a point on the Earth's surface in the northern hemisphere are

  $$\begin{aligned} \frac{\partial u}{\partial t}-f v &=-g \frac{\partial \eta}{\partial x} \\ \frac{\partial v}{\partial t}+f u &=-g \frac{\partial \eta}{\partial y} \\ \frac{\partial \eta}{\partial t} &=-h\left(\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}\right) \end{aligned}$$

  where $u(x, y, t)$ and $v(x, y, t)$ are the horizontal velocity components and $\eta(x, y, t)$ is the perturbation of the height of the free surface.

  (a) Explain the meaning of the three positive constants $f, g$ and $h$ appearing in the equations above and outline the assumptions made in deriving these equations.

  (b) Show that $\zeta$, the $z$-component of vorticity, satisfies

  $$\frac{\partial \zeta}{\partial t}=-f\left(\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}\right)$$

  and deduce that the potential vorticity

  $$q=\zeta-\frac{f}{h} \eta$$

  satisfies

  $$\frac{\partial q}{\partial t}=0$$

  (c) Consider a steady geostrophic flow that is uniform in the latitudinal $(y)$ direction. Show that

  $$\frac{d^{2} \eta}{d x^{2}}-\frac{f^{2}}{g h} \eta=\frac{f}{g} q .$$

  Given that the potential vorticity has the piecewise constant profile

  $$q= \begin{cases}q_{1}, & x<0 \\ q_{2}, & x>0\end{cases}$$

  where $q_{1}$ and $q_{2}$ are constants, and that $v \rightarrow 0$ as $x \rightarrow \pm \infty$, solve for $\eta(x)$ and $v(x)$ in terms of the Rossby radius $R=\sqrt{g h} / f$. Sketch the functions $\eta(x)$ and $v(x)$ in the case $q_{1}>q_{2}$.

  comment

• Paper 3, Section II, C

  Fluid Dynamics

  Part IB, 2019

  A cubic box of side $2 h$, enclosing the region $0<x<2 h, 0<y<2 h,-h<z<h$, contains equal volumes of two incompressible fluids that remain distinct. The system is initially at rest, with the fluid of density $\rho_{1}$ occupying the region $0<z<h$ and the fluid of density $\rho_{2}$ occupying the region $-h<z<0$, and with gravity $(0,0,-g)$. The interface between the fluids is then slightly perturbed. Derive the linearized equations and boundary conditions governing small disturbances to the initial state.

  In the case $\rho_{2}>\rho_{1}$, show that the angular frequencies $\omega$ of the normal modes are given by

  $$\omega^{2}=\left(\frac{\rho_{2}-\rho_{1}}{\rho_{1}+\rho_{2}}\right) g k \tanh (k h)$$

  and express the allowable values of the wavenumber $k$ in terms of $h$. Identify the lowestfrequency non-trivial mode $(\mathrm{s})$. Comment on the limit $\rho_{1} \ll \rho_{2}$. What physical behaviour is expected in the case $\rho_{1}>\rho_{2}$ ?

  comment

• Paper 1, Section II, C

  Fluid Dynamics

  Part IB, 2020

  Steady two-dimensional potential flow of an incompressible fluid is confined to the wedge $0<\theta<\alpha$, where $(r, \theta)$ are polar coordinates centred on the vertex of the wedge and $0<\alpha<\pi$.

  (a) Show that a velocity potential $\phi$ of the form

  $$\phi(r, \theta)=A r^{\gamma} \cos (\lambda \theta),$$

  where $A, \gamma$ and $\lambda$ are positive constants, satisfies the condition of incompressible flow, provided that $\gamma$ and $\lambda$ satisfy a certain relation to be determined.

  Assuming that $u_{\theta}$, the $\theta$-component of velocity, does not change sign within the wedge, determine the values of $\gamma$ and $\lambda$ by using the boundary conditions.

  (b) Calculate the shape of the streamlines of this flow, labelling them by the distance $r_{\min }$ of closest approach to the vertex. Sketch the streamlines.

  (c) Show that the speed $|\mathbf{u}|$ and pressure $p$ are independent of $\theta$. Assuming that at some radius $r=r_{0}$ the speed and pressure are $u_{0}$ and $p_{0}$, respectively, find the pressure difference in the flow between the vertex of the wedge and $r_{0}$.

  [Hint: In polar coordinates $(r, \theta)$,

  $$\nabla f=\left(\frac{\partial f}{\partial r}, \frac{1}{r} \frac{\partial f}{\partial \theta}\right) \quad \text { and } \quad \nabla \cdot \mathbf{F}=\frac{1}{r} \frac{\partial}{\partial r}\left(r F_{r}\right)+\frac{1}{r} \frac{\partial F_{\theta}}{\partial \theta}$$

  for a scalar $f$ and a vector $\mathbf{F}=\left(F_{r}, F_{\theta}\right)$.]

  comment

• Paper 2, Section II, C

  Fluid Dynamics

  Part IB, 2020

  A vertical cylindrical container of radius $R$ is partly filled with fluid of constant density to depth $h$. The free surface is perturbed so that the fluid occupies the region

  $$0<r<R, \quad-h<z<\zeta(r, \theta, t)$$

  where $(r, \theta, z)$ are cylindrical coordinates and $\zeta$ is the perturbed height of the free surface. For small perturbations, a linearised description of surface waves in the cylinder yields the following system of equations for $\zeta$ and the velocity potential $\phi$ :

  $$\begin{aligned} \nabla^{2} \phi &=0, \quad 0<r<R, \quad-h<z<0 \\ \frac{\partial \phi}{\partial t}+g \zeta &=0 \quad \text { on } \quad z=0 \\ \frac{\partial \zeta}{\partial t}-\frac{\partial \phi}{\partial z} &=0 \quad \text { on } \quad z=0 \\ \frac{\partial \phi}{\partial z} &=0 \quad \text { on } \quad z=-h \\ \frac{\partial \phi}{\partial r} &=0 \quad \text { on } \quad r=R \end{aligned}$$

  (a) Describe briefly the physical meaning of each equation.

  (b) Consider axisymmetric normal modes of the form

  $$\phi=\operatorname{Re}\left(\hat{\phi}(r, z) e^{-i \sigma t}\right), \quad \zeta=\operatorname{Re}\left(\hat{\zeta}(r) e^{-i \sigma t}\right)$$

  Show that the system of equations $(1)-(5)$ admits a solution for $\hat{\phi}$ of the form

  $$\hat{\phi}(r, z)=A J_{0}\left(k_{n} r\right) Z(z)$$

  where $A$ is an arbitrary amplitude, $J_{0}(x)$ satisfies the equation

  $$\frac{d^{2} J_{0}}{d x^{2}}+\frac{1}{x} \frac{d J_{0}}{d x}+J_{0}=0$$

  the wavenumber $k_{n}, n=1,2, \ldots$ is such that $x_{n}=k_{n} R$ is one of the zeros of the function $d J_{0} / d x$, and the function $Z(z)$ should be determined explicitly.

  (c) Show that the frequency $\sigma_{n}$ of the $n$-th mode is given by

  $$\sigma_{n}^{2}=\frac{g}{h} \Psi\left(k_{n} h\right)$$

  where the function $\Psi(x)$ is to be determined.

  [Hint: In cylindrical coordinates $(r, \theta, z)$,

  $$\left.\nabla^{2}=\frac{1}{r} \frac{\partial}{\partial r}\left(r \frac{\partial}{\partial r}\right)+\frac{1}{r^{2}} \frac{\partial^{2}}{\partial \theta^{2}}+\frac{\partial^{2}}{\partial z^{2}} \cdot\right]$$

  comment

• Paper 2, Section I, C

  Fluid Dynamics

  Part IB, 2020

  Incompressible fluid of constant viscosity $\mu$ is confined to the region $0<y<h$ between two parallel rigid plates. Consider two parallel viscous flows: flow A is driven by the motion of one plate in the $x$-direction with the other plate at rest; flow B is driven by a constant pressure gradient in the $x$-direction with both plates at rest. The velocity mid-way between the plates is the same for both flows.

  The viscous friction in these flows is known to produce heat locally at a rate

  $$Q=\mu\left(\frac{\partial u}{\partial y}\right)^{2}$$

  per unit volume, where $u$ is the $x$-component of the velocity. Determine the ratio of the total rate of heat production in flow A to that in flow B.

  comment

• Paper 2, Section I, A

  Fluid Dynamics

  Part IB, 2021

  Consider an axisymmetric container, initially filled with water to a depth $h_{I}$. A small circular hole of radius $r_{0}$ is opened in the base of the container at $z=0$.

  (a) Determine how the radius $r$ of the container should vary with $z<h_{I}$ so that the depth of the water will decrease at a constant rate.

  (b) For such a container, determine how the cross-sectional area $A$ of the free surface should decrease with time.

  [You may assume that the flow rate through the opening is sufficiently small that Bernoulli's theorem for steady flows can be applied.]

  comment

• Paper 3, Section I, A

  Fluid Dynamics

  Part IB, 2021

  A two-dimensional flow $\mathbf{u}=(u, v)$ has a velocity field given by

  $$u=\frac{x^{2}-y^{2}}{\left(x^{2}+y^{2}\right)^{2}} \quad \text { and } \quad v=\frac{2 x y}{\left(x^{2}+y^{2}\right)^{2}}$$

  (a) Show explicitly that this flow is incompressible and irrotational away from the origin.

  (b) Find the stream function for this flow.

  (c) Find the velocity potential for this flow.

  comment

• Paper 1, Section II, A

  Fluid Dynamics

  Part IB, 2021

  A two-dimensional flow is given by a velocity potential

  $$\phi(x, y, t)=\epsilon y \sin (x-t)$$

  where $\epsilon$ is a constant.

  (a) Find the corresponding velocity field $\mathbf{u}(x, y, t)$. Determine $\boldsymbol{\nabla} \cdot \mathbf{u}$.

  (b) The time-average $\langle\psi\rangle(x, y)$ of a quantity $\psi(x, y, t)$ is defined as

  $$\langle\psi\rangle(x, y)=\frac{1}{2 \pi} \int_{0}^{2 \pi} \psi(x, y, t) d t .$$

  Show that the time-average of this velocity field is zero everywhere. Write down an expression for the acceleration of fluid particles, and find the time-average of this expression at a fixed point $(x, y)$.

  (c) Now assume that $|\epsilon| \ll 1$. The material particle at $(0,0)$ at $t=0$ is marked with dye. Write down equations for its subsequent motion. Verify that its position $(x, y)$ for $t>0$ is given (correct to terms of order $\epsilon^{2}$ ) by

  $$\begin{aligned} x &=\epsilon^{2}\left(\frac{1}{4} \sin 2 t+\frac{t}{2}-\sin t\right) \\ y &=\epsilon(\cos t-1) \end{aligned}$$

  Deduce the time-average velocity of the dyed particle correct to this order.

  comment

• Paper 3, Section II, A

  Fluid Dynamics

  Part IB, 2021

  A two-dimensional layer of viscous fluid lies between two rigid boundaries at $y=\pm L_{0}$. The boundary at $y=L_{0}$ oscillates in its own plane with velocity $\left(U_{0} \cos \omega t, 0\right)$, while the boundary at $y=-L_{0}$ oscillates in its own plane with velocity $\left(-U_{0} \cos \omega t, 0\right)$. Assume that there is no pressure gradient and that the fluid flows parallel to the boundary with velocity $(u(y, t), 0)$, where $u(y, t)$ can be written as $u(y, t)=\operatorname{Re}\left[U_{0} f(y) \exp (i \omega t)\right]$.

  (a) By exploiting the symmetry of the system or otherwise, show that

  $$f(y)=\frac{\sinh [(1+i) \Delta \hat{y}]}{\sinh [(1+i) \Delta]}, \text { where } \hat{y}=\frac{y}{L_{0}} \text { and } \Delta=\left(\frac{\omega L_{0}^{2}}{2 \nu}\right)^{1 / 2}$$

  (b) Hence or otherwise, show that

  where $\Delta_{\pm}=\Delta(1 \pm \hat{y})$.

  (c) Show that, for $\Delta \ll 1$,

  $$u(y, t) \simeq \frac{U_{0} y}{L_{0}} \cos \omega t$$

  and briefly interpret this result physically.

  $$\begin{aligned} & \frac{u(y, t)}{U_{0}}=\frac{\cos \omega t\left[\cosh \Delta_{+} \cos \Delta_{-}-\cosh \Delta_{-} \cos \Delta_{+}\right]}{(\cosh 2 \Delta-\cos 2 \Delta)} \\ & +\frac{\sin \omega t\left[\sinh \Delta_{+} \sin \Delta_{-}-\sinh \Delta_{-} \sin \Delta_{+}\right]}{(\cosh 2 \Delta-\cos 2 \Delta)}, \end{aligned}$$

  comment

• Paper 4, Section II, A

  Fluid Dynamics

  Part IB, 2021

  Consider the spherically symmetric motion induced by the collapse of a spherical cavity of radius $a(t)$, centred on the origin. For $r<a$, there is a vacuum, while for $r>a$, there is an inviscid incompressible fluid with constant density $\rho$. At time $t=0, a=a_{0}$, and the fluid is at rest and at constant pressure $p_{0}$.

  (a) Consider the radial volume transport in the fluid $Q(R, t)$, defined as

  $$Q(R, t)=\int_{r=R} u d S$$

  where $u$ is the radial velocity, and $d S$ is an infinitesimal element of the surface of a sphere of radius $R \geqslant a$. Use the incompressibility condition to establish that $Q$ is a function of time alone.

  (b) Using the expression for pressure in potential flow or otherwise, establish that

  $$\frac{1}{4 \pi a} \frac{d Q}{d t}-\frac{(\dot{a})^{2}}{2}=-\frac{p_{0}}{\rho}$$

  where $\dot{a}(t)$ is the radial velocity of the cavity boundary.

  (c) By expressing $Q(t)$ in terms of $a$ and $\dot{a}$, show that

  $$\dot{a}=-\sqrt{\frac{2 p_{0}}{3 \rho}\left(\frac{a_{0}^{3}}{a^{3}}-1\right)}$$

  [Hint: You may find it useful to assume $\dot{a}(t)$ is an explicit function of a from the outset.]

  (d) Hence write down an integral expression for the implosion time $\tau$, i.e. the time for the radius of the cavity $a \rightarrow 0$. [Do not attempt to evaluate the integral.]

  comment

• Paper 4, Section II, A

  Fluid Dynamics

  Part II, 2019

  (a) Show that the Stokes flow around a rigid moving sphere has the minimum viscous dissipation rate of all incompressible flows which satisfy the no-slip boundary conditions on the sphere.

  (b) Let $\boldsymbol{u}=\boldsymbol{\nabla}(\boldsymbol{x} \cdot \boldsymbol{\Phi}+\chi)-2 \boldsymbol{\Phi}$, where $\boldsymbol{\Phi}$ and $\chi$ are solutions of Laplace's equation, i.e. $\nabla^{2} \boldsymbol{\Phi}=\mathbf{0}$ and $\nabla^{2} \chi=0$.

  (i) Show that $\boldsymbol{u}$ is incompressible.

  (ii) Show that $\boldsymbol{u}$ satisfies Stokes equation if the pressure $p=2 \mu \boldsymbol{\nabla} \cdot \boldsymbol{\Phi}$.

  (c) Consider a rigid sphere moving with velocity $\boldsymbol{U}$. The Stokes flow around the sphere is given by

  $$\boldsymbol{\Phi}=\alpha \frac{\boldsymbol{U}}{r} \quad \text { and } \quad \chi=\beta \boldsymbol{U} \cdot \boldsymbol{\nabla}\left(\frac{1}{r}\right)$$

  where the origin is chosen to be at the centre of the sphere. Find the values for $\alpha$ and $\beta$ which ensure no-slip conditions are satisfied on the sphere.

  comment

• Paper 2, Section II, A

  Fluid Dynamics

  Part II, 2019

  A viscous fluid is contained in a channel between rigid planes $y=-h$ and $y=h$. The fluid in the upper region $\sigma<y<h$ (with $-h<\sigma<h$ ) has dynamic viscosity $\mu_{-}$ while the fluid in the lower region $-h<y<\sigma$ has dynamic viscosity $\mu_{+}>\mu_{-}$. The plane at $y=h$ moves with velocity $U_{-}$and the plane at $y=-h$ moves with velocity $U_{+}$, both in the $x$ direction. You may ignore the effect of gravity.

  (a) Find the steady, unidirectional solution of the Navier-Stokes equations in which the interface between the two fluids remains at $y=\sigma$.

  (b) Using the solution from part (a):

  (i) calculate the stress exerted by the fluids on the two boundaries;

  (ii) calculate the total viscous dissipation rate in the fluids;

  (iii) demonstrate that the rate of working by boundaries balances the viscous dissipation rate in the fluids.

  (c) Consider the situation where $U_{+}+U_{-}=0$. Defining the volume flux in the upper region as $Q_{-}$and the volume flux in the lower region as $Q_{+}$, show that their ratio is independent of $\sigma$ and satisfies

  $$\frac{Q_{-}}{Q_{+}}=-\frac{\mu_{-}}{\mu_{+}}$$

  comment

• Paper 3, Section II, A

  Fluid Dynamics

  Part II, 2019

  For a fluid with kinematic viscosity $\nu$, the steady axisymmetric boundary-layer equations for flow primarily in the $z$-direction are

  $$\begin{aligned} u \frac{\partial w}{\partial r}+w \frac{\partial w}{\partial z} &=\frac{\nu}{r} \frac{\partial}{\partial r}\left(r \frac{\partial w}{\partial r}\right) \\ \frac{1}{r} \frac{\partial(r u)}{\partial r}+\frac{\partial w}{\partial z} &=0 \end{aligned}$$

  where $u$ is the fluid velocity in the $r$-direction and $w$ is the fluid velocity in the $z$-direction. A thin, steady, axisymmetric jet emerges from a point at the origin and flows along the $z$-axis in a fluid which is at rest far from the $z$-axis.

  (a) Show that the momentum flux

  $$M:=\int_{0}^{\infty} r w^{2} d r$$

  is independent of the position $z$ along the jet. Deduce that the thickness $\delta(z)$ of the jet increases linearly with $z$. Determine the scaling dependence on $z$ of the centre-line velocity $W(z)$. Hence show that the jet entrains fluid.

  (b) A similarity solution for the streamfunction,

  $$\psi(x, y, z)=\nu z g(\eta) \quad \text { with } \quad \eta:=r / z$$

  exists if $g$ satisfies the second order differential equation

  $$\eta g^{\prime \prime}-g^{\prime}+g g^{\prime}=0$$

  Using appropriate boundary and normalisation conditions (which you should state clearly) to solve this equation, show that

  $$g(\eta)=\frac{12 M \eta^{2}}{32 \nu^{2}+3 M \eta^{2}}$$

  comment

• Paper 1, Section II, A

  Fluid Dynamics

  Part II, 2019

  A disc of radius $R$ and weight $W$ hovers at a height $h$ on a cushion of air above a horizontal air table - a fine porous plate through which air of density $\rho$ and dynamic viscosity $\mu$ is pumped upward at constant speed $V$. You may assume that the air flow is axisymmetric with no flow in the azimuthal direction, and that the effect of gravity on the air may be ignored.

  (a) Write down the relevant components of the Navier-Stokes equations. By estimating the size of the individual terms, simplify these equations when $\varepsilon:=h / R \ll 1$ and $R e:=\rho V h / \mu \ll 1$.

  (b) Explain briefly why it is reasonable to expect that the vertical velocity of the air below the disc is a function of distance above the air table alone, and thus find the steady pressure distribution below the disc. Hence show that

  $$W=\frac{3 \pi \mu V R}{2 \varepsilon^{3}}$$

  comment

• Paper 1, Section II, 39A II

  Fluid Dynamics

  Part II, 2021

  (a) Write down the Stokes equations for the motion of an incompressible viscous fluid with negligible inertia (in the absence of body forces). What does it mean that Stokes flow is linear and reversible?

  (b) The region $a<r<b$ between two concentric rigid spheres of radii $a$ and $b$ is filled with fluid of large viscosity $\mu$. The outer sphere is held stationary, while the inner sphere is made to rotate with angular velocity $\boldsymbol{\Omega}$.

  (i) Use symmetry and the properties of Stokes flow to deduce that $p=0$, where $p$ is the pressure due to the flow.

  (ii) Verify that both solid-body rotation and $\mathbf{u}(\mathbf{x})=\boldsymbol{\Omega} \wedge \boldsymbol{\nabla}(1 / r)$ satisfy the Stokes equations with $p=0$. Hence determine the fluid velocity between the spheres.

  (iii) Calculate the stress tensor $\sigma_{i j}$ in the flow.

  (iv) Deduce that the couple $\mathbf{G}$ exerted by the fluid in $r<c$ on the fluid in $r>c$, where $a<c<b$, is given by

  $$\mathbf{G}=\frac{8 \pi \mu a^{3} b^{3} \mathbf{\Omega}}{b^{3}-a^{3}}$$

  independent of the value of $c$. [Hint: Do not substitute the form of $A$ and $B$ in $A+B r^{-3}$ until the end of the calculation.]

  Comment on the form of this result for $a \ll b$ and for $b-a \ll a$.

  $\left[Y o u\right.$ may use $\int_{r=R} n_{i} n_{j} d S=\frac{4}{3} \pi R^{2} \delta_{i j}$, where $\mathbf{n}$ is the normal to $\left.r=R .\right]$

  comment

• Paper 2, Section II, 39A II

  Fluid Dynamics

  Part II, 2021

  (a) Incompressible fluid of viscosity $\mu$ fills the thin, slowly varying gap between rigid boundaries at $z=0$ and $z=h(x, y)>0$. The boundary at $z=0$ translates in its own plane with a constant velocity $\mathbf{U}=(U, 0,0)$, while the other boundary is stationary. If $h$ has typical magnitude $H$ and varies on a lengthscale $L$, state conditions for the lubrication approximation to be appropriate.

  Write down the lubrication equations for this problem and show that the horizontal volume flux $\mathbf{q}=\left(q_{x}, q_{y}, 0\right)$ is given by

  $$\mathbf{q}=\frac{\mathbf{U} h}{2}-\frac{h^{3}}{12 \mu} \nabla p$$

  where $p(x, y)$ is the pressure.

  Explain why $\mathbf{q}=\nabla \wedge(0,0, \psi)$ for some function $\psi(x, y)$. Deduce that $\psi$ satisfies the equation

  $$\nabla \cdot\left(\frac{1}{h^{3}} \nabla \psi\right)=-\frac{U}{h^{3}} \frac{\partial h}{\partial y}$$

  (b) Now consider the case $\mathbf{U}=\mathbf{0}, h=h_{0}$ for $r>a$ and $h=h_{1}$ for $r<a$, where $h_{0}, h_{1}$ and $a$ are constants, and $(r, \theta)$ are polar coordinates. A uniform pressure gradient $\nabla p=-G \mathbf{e}_{x}$ is applied at infinity. Show that $\psi \sim A r \sin \theta$ as $r \rightarrow \infty$, where the constant $A$ is to be determined.

  Given that $a \gg h_{0}, h_{1}$, you may assume that the equations of part (a) apply for $r<a$ and $r>a$, and are subject to conditions that the radial component $q_{r}$ of the volume flux and the pressure $p$ are both continuous across $r=a$. Show that these continuity conditions imply that

  $$\left[\frac{\partial \psi}{\partial \theta}\right]_{-}^{+}=0 \quad \text { and }\left[\frac{1}{h^{3}} \frac{\partial \psi}{\partial r}\right]_{-}^{+}=0$$

  respectively, where []$_{-}^{+}$denotes the jump across $r=a$.

  Hence determine $\psi(r, \theta)$ and deduce that the total flux through $r=a$ is given by

  $$\frac{4 A a h_{1}^{3}}{h_{0}^{3}+h_{1}^{3}}$$

  comment

• Paper 3, Section II, 38A II

  Fluid Dynamics

  Part II, 2021

  Viscous fluid occupying $z>0$ is bounded by a rigid plane at $z=0$ and is extracted through a small hole at the origin at a constant flow rate $Q=2 \pi A$. Assume that for sufficiently small values of $R=|\mathbf{x}|$ the velocity $\mathbf{u}(\mathbf{x})$ is well-approximated by

  $$\mathbf{u}=-\frac{A \mathbf{x}}{R^{3}}$$

  except within a thin axisymmetric boundary layer near $z=0$.

  (a) Estimate the Reynolds number of the flow as a function of $R$, and thus give an estimate for how small $R$ needs to be for such a solution to be applicable. Show that the radial pressure gradient is proportional to $R^{-5}$.

  (b) In cylindrical polar coordinates $(r, \theta, z)$, the steady axisymmetric boundary-layer equations for the velocity components $(u, 0, w)$ can be written as

  $$u \frac{\partial u}{\partial r}+w \frac{\partial u}{\partial z}=-\frac{1}{\rho} \frac{d P}{d r}+\nu \frac{\partial^{2} u}{\partial z^{2}}, \quad \text { where } \quad u=-\frac{1}{r} \frac{\partial \Psi}{\partial z}, \quad w=\frac{1}{r} \frac{\partial \Psi}{\partial r}$$

  and $\Psi(r, z)$ is the Stokes streamfunction. Verify that the condition of incompressibility is satisfied by the use of $\Psi$.

  Use scaling arguments to estimate the thickness $\delta(r)$ of the boundary layer near $z=0$ and then to motivate seeking a similarity solution of the form

  $$\Psi=(A \nu r)^{1 / 2} F(\eta), \quad \text { where } \quad \eta=z / \delta(r)$$

  (c) Obtain the differential equation satisfied by $F$, and state the conditions that would determine its solution. [You are not required to find this solution.]

  By considering the flux in the boundary layer, explain why there should be a correction to the approximation $(*)$ of relative magnitude $(\nu R / A)^{1 / 2} \ll 1$.

  comment

• Paper 4, Section II, A II

  Fluid Dynamics

  Part II, 2021

  Consider a steady axisymmetric flow with components $(-\alpha r, v(r), 2 \alpha z)$ in cylindrical polar coordinates $(r, \theta, z)$, where $\alpha$ is a positive constant. The fluid has density $\rho$ and kinematic viscosity $\nu$.

  (a) Briefly describe the flow and confirm that it is incompressible.

  (b) Show that the vorticity has one component $\omega(r)$, in the $z$ direction. Write down the corresponding vorticity equation and derive the solution

  $$\omega=\omega_{0} e^{-\alpha r^{2} /(2 \nu)}$$

  Hence find $v(r)$ and show that it has a maximum at some finite radius $r^{*}$, indicating how $r^{*}$ scales with $\nu$ and $\alpha$.

  (c) Find an expression for the net advection of angular momentum, prv, into the finite cylinder defined by $r \leqslant r_{0}$ and $-z_{0} \leqslant z \leqslant z_{0}$. Show that this is always positive and asymptotes to the value

  $$\frac{8 \pi \rho z_{0} \omega_{0} \nu^{2}}{\alpha}$$

  as $r_{0} \rightarrow \infty$

  (d) Show that the torque exerted on the cylinder of part (c) by the exterior flow is always negative and demonstrate that it exactly balances the net advection of angular momentum. Comment on why this has to be so.

  [You may assume that for a flow $(u, v, w)$ in cylindrical polar coordinates

  $$\begin{aligned} & e_{r \theta}=\frac{r}{2} \frac{\partial}{\partial r}\left(\frac{v}{r}\right)+\frac{1}{2 r} \frac{\partial u}{\partial \theta}, \quad e_{\theta z}=\frac{1}{2 r} \frac{\partial w}{\partial \theta}+\frac{1}{2} \frac{\partial v}{\partial z}, \quad e_{r z}=\frac{1}{2} \frac{\partial u}{\partial z}+\frac{1}{2} \frac{\partial w}{\partial r} \\ & \text { and } \left.\boldsymbol{\omega}=\frac{1}{r}\left|\begin{array}{ccc}\mathbf{e}_{r} & r \mathbf{e}_{\theta} & \mathbf{e}_{z} \\\partial / \partial r & \partial / \partial \theta & \partial / \partial z \\u & r v & w\end{array}\right| .\right] \end{aligned}$$

  comment